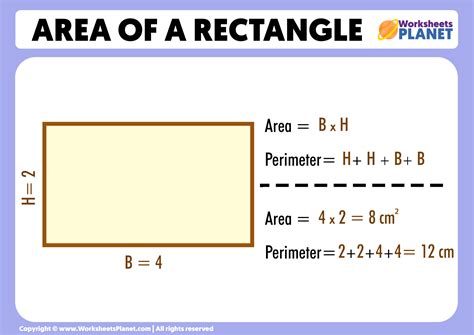
Calculating the area of various shapes is a fundamental concept in geometry, crucial for numerous real-world applications, including architecture, engineering, and design. Understanding how to find the area of different shapes, such as triangles, rectangles, circles, and more, can significantly simplify tasks in these fields. The process involves applying specific formulas tailored to each shape's characteristics. For instance, the area of a rectangle is found by multiplying its length by its width, while the area of a circle requires using the formula πr^2, where r is the radius of the circle.
Understanding Basic Shapes and Their Area Formulas

To find the area easily, it’s essential to grasp the basic formulas for common shapes. The area of a triangle, for example, can be calculated using the formula: Area = (base * height) / 2. This formula applies to all types of triangles, whether they are right-angled, isosceles, or scalene. For rectangles and squares, the area is calculated as length times width, with the distinction being that a square has all sides of equal length. Circles, on the other hand, require the use of π (pi) in their area formula: Area = π * r^2, where r is the radius. These basic formulas are the building blocks for calculating the areas of more complex shapes.
Calculating the Area of Complex Shapes
For more complex shapes, such as trapezoids, ellipses, and polygons, the area calculations can be more involved. The area of a trapezoid, for instance, is found using the formula: Area = ((a + b) / 2) * h, where ‘a’ and ‘b’ are the lengths of the two parallel sides, and ‘h’ is the height between them. Ellipses, which are essentially stretched circles, have an area formula that involves both the lengths of their semi-major and semi-minor axes: Area = π * a * b, where ‘a’ and ‘b’ are the lengths of the semi-major and semi-minor axes, respectively. Polygons, depending on their regularity and the number of sides, may require breaking them down into simpler shapes like triangles and rectangles to calculate their total area.
Key Points
- The area of basic shapes like triangles, rectangles, and circles can be calculated using specific formulas.
- For triangles, the area formula is (base * height) / 2.
- Rectangles and squares use the formula length * width, with squares having all sides equal.
- Circles require the formula π * r^2, where r is the radius.
- Complex shapes like trapezoids, ellipses, and polygons may involve more intricate formulas or breaking down into simpler shapes.
| Shape | Area Formula |
|---|---|
| Triangle | (base * height) / 2 |
| Rectangle/Square | length * width |
| Circle | π * r^2 |
| Trapezoid | ((a + b) / 2) * h |
| Ellipse | π * a * b |
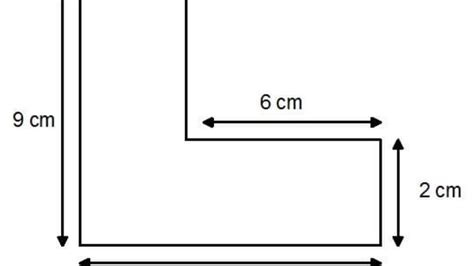
Real-World Applications of Area Calculations
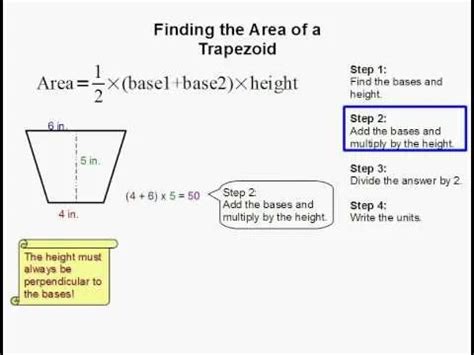
In practical scenarios, calculating areas is essential for various tasks, such as designing rooms, building houses, creating art, and engineering structures. For architects, knowing the area of a room or a building site is crucial for planning the layout and ensuring that the space meets the functional and aesthetic needs of the occupants. In construction, accurate area calculations are vital for ordering the correct amount of materials, such as flooring, roofing, and paint, thus helping to control costs and prevent waste. Artists and designers use area calculations to create balanced compositions and to ensure that their work fits within the intended space.
Technological Tools for Area Calculations
With the advent of technology, calculating areas has become more efficient and accurate. Software programs and apps designed for architecture, engineering, and design can quickly calculate areas of complex shapes and provide detailed analyses of spatial arrangements. These tools not only save time but also reduce the likelihood of human error, making them indispensable in professional settings. Moreover, online calculators and educational software have made it easier for students and hobbyists to learn and apply area calculation principles without needing to perform tedious manual calculations.
What is the formula for the area of a triangle?
+The area of a triangle is calculated using the formula: Area = (base * height) / 2.
How do you calculate the area of a circle?
+The area of a circle is found using the formula: Area = π * r^2, where r is the radius of the circle.
What is the importance of calculating areas in real-world applications?
+Calculating areas is crucial for tasks such as designing spaces, planning constructions, and creating art. It helps in ensuring functional and aesthetic needs are met, in managing resources efficiently, and in achieving balanced compositions.
In conclusion, finding the area of shapes is a fundamental skill that underpins various aspects of geometry and has numerous practical applications. By understanding and applying the appropriate formulas for different shapes, individuals can simplify complex tasks and ensure accuracy in their calculations. Whether in professional fields like architecture and engineering or in personal projects, the ability to calculate areas effectively is a valuable skill that can lead to more efficient and successful outcomes.