Absolute value is a fundamental concept in mathematics, particularly in algebra and calculus. It represents the distance of a number from zero on the number line, without considering whether the number is positive or negative. The absolute value of a number x is denoted by |x| and is defined as the non-negative value of x without regard to its sign. In this article, we will explore five ways absolute value is used in mathematics and real-world applications, highlighting its significance and versatility.
Key Points
- Absolute value represents the distance of a number from zero on the number line.
- It is used in solving equations and inequalities, particularly those involving quadratic expressions.
- Absolute value functions are crucial in graphing and analyzing linear and non-linear relationships.
- In real-world applications, absolute value is used in distance calculations, such as determining the distance between two points in a coordinate system.
- It also plays a significant role in computer programming and data analysis, especially when dealing with error margins and deviations from expected values.
Solving Equations and Inequalities

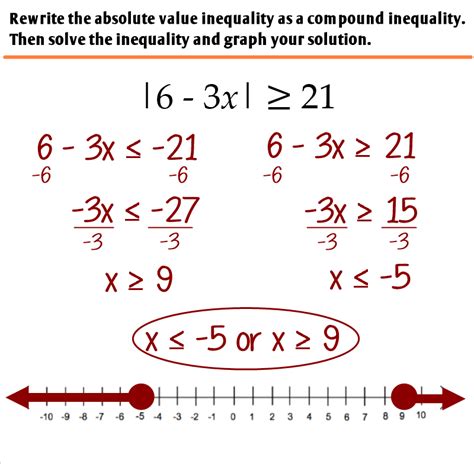
Absolute value is essential in solving equations and inequalities. When dealing with absolute value equations, such as |x| = 5, the solution involves finding the values of x that satisfy the equation, which in this case are x = 5 and x = -5. Similarly, absolute value inequalities, like |x| > 3, require finding all values of x that are more than 3 units away from zero on the number line, which would be x < -3 or x > 3. The use of absolute value in these contexts allows for the consideration of both positive and negative solutions, making it a powerful tool in algebraic problem-solving.
Graphing Absolute Value Functions
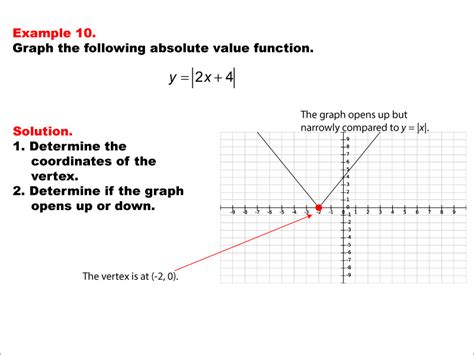
Absolute value functions, such as f(x) = |x|, have distinct graphs that reflect their definition. The graph of f(x) = |x| is a V-shaped graph that is symmetric about the y-axis and opens upwards, with its vertex at (0,0). This characteristic shape helps in understanding the behavior of absolute value functions and is critical in analyzing linear and non-linear relationships in mathematics and real-world phenomena. For instance, the absolute value function can model the cost of producing a certain quantity of goods, where the cost increases as the quantity moves away from a certain optimal level.
| Function Type | Description |
|---|---|
| Linear | Represents a straight line, often used to model constant rates of change. |
| Absolute Value | Characterized by a V-shaped graph, useful for modeling situations where the rate of change is not constant but depends on the distance from a reference point. |
| Quadratic | Describes a parabolic shape, commonly used in physics and engineering to model trajectories and energy levels. |

Real-World Applications
Absolute value has numerous practical applications across various fields. In physics, it is used to calculate distances and speeds, which are essential in understanding motion and energy transfer. For example, the absolute value of the velocity of an object gives its speed, which is a critical parameter in determining the object’s kinetic energy and its ability to perform work. In economics, absolute value can be used to analyze the impact of changes in supply and demand on market prices, providing insights into how economies respond to shocks and fluctuations.
Computer Programming and Data Analysis
In computer programming and data analysis, absolute value is used to deal with error margins and deviations from expected values. For instance, when calculating the average of a set of numbers, the absolute deviation of each number from the mean can be used to understand the spread of the data. This is particularly useful in quality control, where understanding deviations from a standard or expected value is crucial for maintaining high product quality and reliability.
In conclusion, absolute value is a versatile and essential concept in mathematics, with applications ranging from solving equations and inequalities to modeling real-world phenomena and analyzing data. Its ability to represent distances and magnitudes without regard to direction makes it a fundamental tool in various fields, including physics, economics, and computer science. As mathematics continues to evolve and play a more significant role in understanding and describing the world around us, the importance of absolute value and its applications will only continue to grow.
What is the definition of absolute value?
+Absolute value refers to the distance of a number from zero on the number line, without considering its sign. It is denoted by |x| and is always non-negative.
How is absolute value used in solving equations?
+Absolute value is used in solving equations by considering both positive and negative solutions. For example, the equation |x| = 5 has solutions x = 5 and x = -5.
What are some real-world applications of absolute value?
+Absolute value has applications in physics for calculating distances and speeds, in economics for analyzing market trends, and in computer programming for dealing with error margins and data analysis.