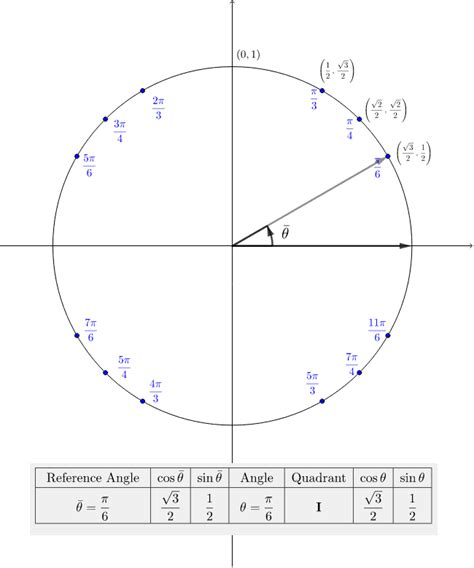
The unit circle is a fundamental concept in mathematics, particularly in trigonometry and geometry. It is a circle with a radius of 1 unit, centered at the origin (0, 0) of a coordinate plane. The unit circle is divided into four quadrants, each representing a specific range of angles and coordinates. Understanding the unit circle quadrants is crucial for solving trigonometric problems, graphing functions, and visualizing mathematical relationships.
The four quadrants of the unit circle are labeled as follows: Quadrant I (upper right), Quadrant II (upper left), Quadrant III (lower left), and Quadrant IV (lower right). Each quadrant corresponds to a specific range of angles, measured counterclockwise from the positive x-axis. The angles in each quadrant are as follows: Quadrant I (0° to 90°), Quadrant II (90° to 180°), Quadrant III (180° to 270°), and Quadrant IV (270° to 360° or 0°).
Key Points
- The unit circle is a circle with a radius of 1 unit, centered at the origin (0, 0) of a coordinate plane.
- The unit circle is divided into four quadrants: Quadrant I (upper right), Quadrant II (upper left), Quadrant III (lower left), and Quadrant IV (lower right).
- Each quadrant corresponds to a specific range of angles, measured counterclockwise from the positive x-axis.
- Understanding the unit circle quadrants is crucial for solving trigonometric problems, graphing functions, and visualizing mathematical relationships.
- The unit circle quadrants are used to determine the signs of trigonometric functions, such as sine, cosine, and tangent.
Quadrant I: Upper Right
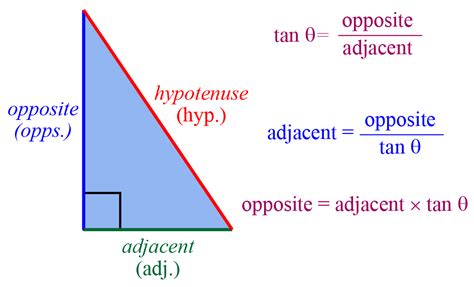
Quadrant I is the upper right quadrant, where both x and y coordinates are positive. The angles in this quadrant range from 0° to 90°. The trigonometric functions in Quadrant I are all positive, meaning that the sine, cosine, and tangent values are all positive.
Trigonometric Functions in Quadrant I
In Quadrant I, the sine function increases from 0 to 1, the cosine function decreases from 1 to 0, and the tangent function increases from 0 to infinity. The following table summarizes the trigonometric functions in Quadrant I:
| Angle | Sine | Cosine | Tangent |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 0.5 | 0.866 | 0.577 |
| 60° | 0.866 | 0.5 | 1.732 |
| 90° | 1 | 0 | ∞ |
Quadrant II: Upper Left
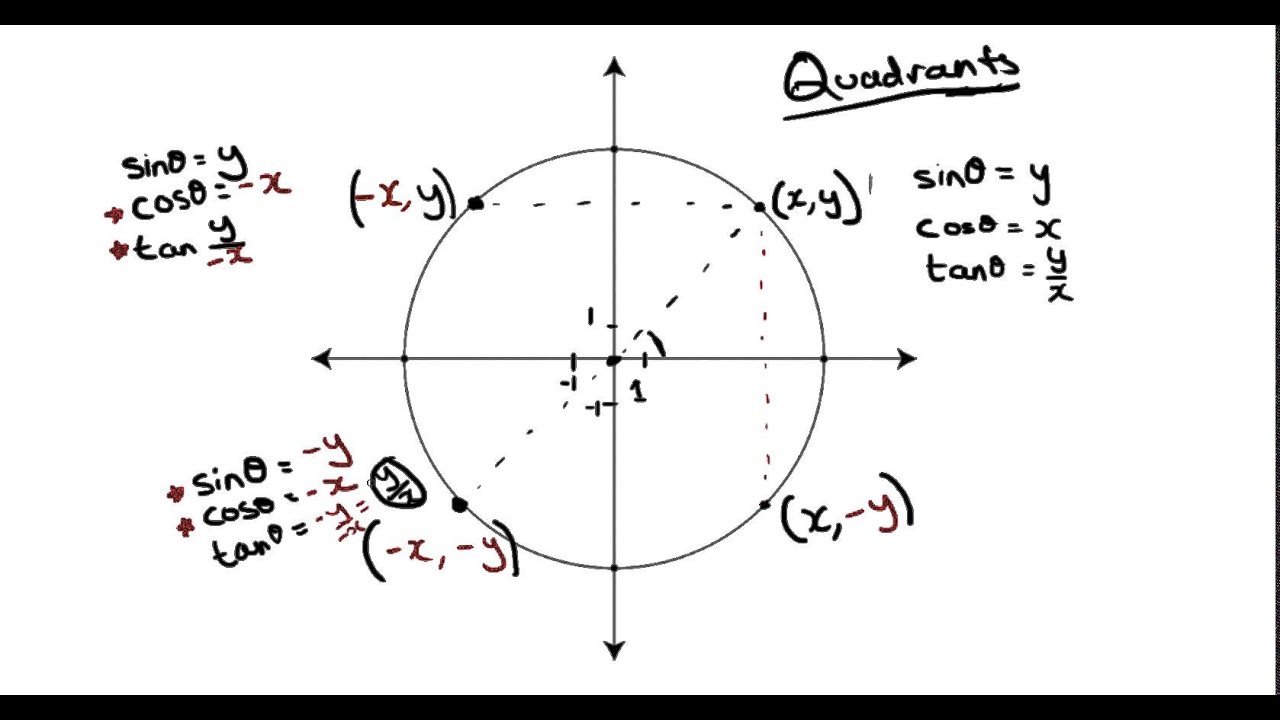
Quadrant II is the upper left quadrant, where the x-coordinate is negative and the y-coordinate is positive. The angles in this quadrant range from 90° to 180°. The trigonometric functions in Quadrant II have the following signs: sine is positive, cosine is negative, and tangent is negative.
Trigonometric Functions in Quadrant II
In Quadrant II, the sine function decreases from 1 to 0, the cosine function decreases from 0 to -1, and the tangent function decreases from infinity to 0. The following table summarizes the trigonometric functions in Quadrant II:
| Angle | Sine | Cosine | Tangent |
|---|---|---|---|
| 90° | 1 | 0 | ∞ |
| 120° | 0.866 | -0.5 | -1.732 |
| 150° | 0.5 | -0.866 | -0.577 |
| 180° | 0 | -1 | 0 |
Quadrant III: Lower Left
Quadrant III is the lower left quadrant, where both x and y coordinates are negative. The angles in this quadrant range from 180° to 270°. The trigonometric functions in Quadrant III have the following signs: sine is negative, cosine is negative, and tangent is positive.
Trigonometric Functions in Quadrant III
In Quadrant III, the sine function decreases from 0 to -1, the cosine function decreases from -1 to 0, and the tangent function increases from 0 to infinity. The following table summarizes the trigonometric functions in Quadrant III:
| Angle | Sine | Cosine | Tangent |
|---|---|---|---|
| 180° | 0 | -1 | 0 |
| 210° | -0.5 | -0.866 | 0.577 |
| 240° | -0.866 | -0.5 | 1.732 |
| 270° | -1 | 0 | ∞ |
Quadrant IV: Lower Right
Quadrant IV is the lower right quadrant, where the x-coordinate is positive and the y-coordinate is negative. The angles in this quadrant range from 270° to 360° or 0°. The trigonometric functions in Quadrant IV have the following signs: sine is negative, cosine is positive, and tangent is negative.
Trigonometric Functions in Quadrant IV
In Quadrant IV, the sine function increases from -1 to 0, the cosine function increases from 0 to 1, and the tangent function decreases from infinity to 0. The following table summarizes the trigonometric functions in Quadrant IV:
| Angle | Sine | Cosine | Tangent |
|---|---|---|---|
| 270° | -1 | 0 | ∞ |
| 300° | -0.866 | 0.5 | -1.732 |
| 330° | -0.5 | 0.866 | -0.577 |
| 360° or 0° | 0 | 1 | 0 |
What is the unit circle, and why is it important in mathematics?
+The unit circle is a circle with a radius of 1 unit, centered at the origin (0, 0) of a coordinate plane. It is essential in mathematics because it helps to define the trigonometric functions, such as sine, cosine, and tangent, and provides a framework for understanding the relationships between angles and coordinates.
How do the unit circle quadrants relate to the trigonometric functions?
+The unit circle quadrants determine the signs of the trigonometric functions. For example, in Quadrant I, all trigonometric functions are positive, while in Quadrant II, the sine function is positive, and the cosine and tangent functions are negative.
What are some real-world applications of the unit circle and its quadrants?
+The unit circle and its quadrants have numerous real-world applications in fields such as physics, engineering, navigation, and computer graphics. They are used to model periodic phenomena, such as sound waves and light waves, and to describe the motion of objects in two-dimensional space.
In conclusion, the unit circle quadrants are a fundamental concept in mathematics, providing a framework for understanding the relationships between angles, coordinates, and trigonometric functions. By recognizing the patterns and relationships between the quadrants, you can simplify complex trigonometric expressions and solve problems more efficiently. The unit circle and its quadrants have numerous real-world applications, making them an essential tool for anyone working in mathematics, science, or engineering.