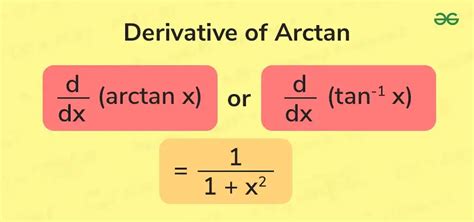
The derivative of arctan, denoted as $\frac{d}{dx} \arctan(x)$, is a fundamental concept in calculus, particularly in the realm of inverse trigonometric functions. The arctan function, also known as the inverse tangent function, is used to determine the angle whose tangent is a given number. Understanding its derivative is crucial for various applications in physics, engineering, and mathematics, where rates of change and optimization are key considerations.
Key Points
- The derivative of arctan(x) is $\frac{1}{1+x^2}$, which represents the rate of change of the arctan function with respect to x.
- This derivative is used in numerous mathematical and scientific applications, including optimization problems and the analysis of rates of change in physical systems.
- The arctan function and its derivative are closely related to the tangent function and its derivative, showcasing the intrinsic connections between trigonometric and inverse trigonometric functions.
- Calculating the derivative of arctan involves using the definition of the derivative as a limit, along with trigonometric identities, particularly the Pythagorean identity for tangent and secant.
- The derivative of arctan is essential in the development of more complex mathematical theories and models, such as those involving calculus of variations and differential equations.
Derivation of the Derivative of Arctan

To derive the derivative of arctan(x), we start with the definition of the arctan function as the inverse of the tangent function. Let y = \arctan(x); then, x = \tan(y). By differentiating both sides with respect to x, we apply the chain rule to the right side, considering \frac{d}{dx} \tan(y), which involves \frac{dy}{dx} because y is a function of x.
The derivative of $\tan(y)$ with respect to y is $\sec^2(y)$, so by the chain rule, we have $\frac{d}{dx} \tan(y) = \sec^2(y) \cdot \frac{dy}{dx}$. Given $x = \tan(y)$, this derivative is equal to 1 (since we're differentiating with respect to x), leading to $1 = \sec^2(y) \cdot \frac{dy}{dx}$. Solving for $\frac{dy}{dx}$ gives $\frac{dy}{dx} = \frac{1}{\sec^2(y)}$.
Substituting $y = \arctan(x)$ back into the equation and recognizing that $\sec^2(y) = 1 + \tan^2(y)$, we find $\sec^2(\arctan(x)) = 1 + \tan^2(\arctan(x)) = 1 + x^2$, because $\tan(\arctan(x)) = x$. Thus, the derivative $\frac{dy}{dx} = \frac{1}{1+x^2}$.
Applications of the Derivative of Arctan
The derivative of arctan has numerous applications in calculus, particularly in optimization problems and in the analysis of functions’ behaviors. It is also crucial in the study of trigonometric and inverse trigonometric functions, showcasing how rates of change can be calculated for these functions. For example, in physics, the derivative of arctan can be used to model the angle of elevation of a projectile under the influence of gravity, where the rate of change of this angle with respect to time or distance is of interest.
| Function | Derivative |
|---|---|
| arctan(x) | $\frac{1}{1+x^2}$ |
| tan(x) | $\sec^2(x)$ |
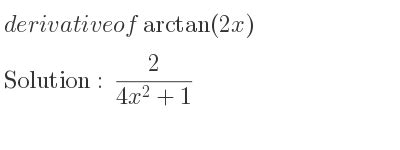
Calculus Applications and Extensions

Beyond its direct applications, the derivative of arctan is a foundational element in more advanced calculus topics, such as the study of differential equations and calculus of variations. In these contexts, understanding how functions change and optimize is essential for solving complex problems that arise in physics, engineering, and economics.
The relationship between the arctan function and its derivative also provides a platform for exploring deeper mathematical concepts, such as the properties of inverse functions and the behavior of trigonometric functions in the complex plane. This depth of understanding is crucial for professionals and researchers working in fields that rely heavily on mathematical modeling and analysis.
Mathematical and Computational Considerations
In computational mathematics and numerical analysis, the derivative of arctan is used in algorithms for solving equations and optimizing functions. The precision and efficiency of these algorithms often depend on the accurate calculation of derivatives, making the derivative of arctan a critical component in software and programming related to mathematical and scientific computing.
What is the primary use of the derivative of arctan in calculus?
+The primary use of the derivative of arctan in calculus is to find the rate of change of the arctan function with respect to its input, which is essential for optimization problems, analyzing the behavior of functions, and modeling physical phenomena.
How does the derivative of arctan relate to the tangent function?
+The derivative of arctan is closely related to the tangent function because arctan is the inverse function of tangent. The derivative of arctan(x) is $\frac{1}{1+x^2}$, which reflects the reciprocal relationship between the derivatives of inverse functions.
What are some practical applications of the derivative of arctan?
+Practical applications of the derivative of arctan include optimization problems in economics and physics, modeling the trajectory of projectiles, and analyzing the behavior of signals in telecommunications and signal processing.
In conclusion, the derivative of arctan is a fundamental concept in calculus with a wide range of applications in mathematics, physics, and engineering. Its calculation and understanding are crucial for any professional or researcher working in fields that involve mathematical modeling, optimization, and the analysis of rates of change. The derivative of arctan not only serves as a tool for solving specific problems but also deepens our understanding of the intrinsic relationships between trigonometric and inverse trigonometric functions, contributing to the richness and complexity of mathematical theory and its applications.