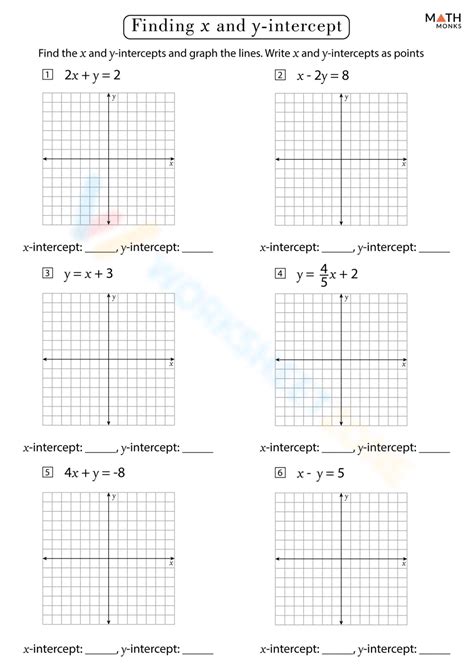
The y-intercept is a fundamental concept in algebra and geometry, representing the point at which a line or curve intersects the y-axis. It is a crucial element in understanding the behavior and position of linear equations and functions. Finding the y-intercept can be accomplished through two primary methods: using the slope-intercept form of a linear equation and substituting x=0 into the equation of the line.
Understanding the Slope-Intercept Form
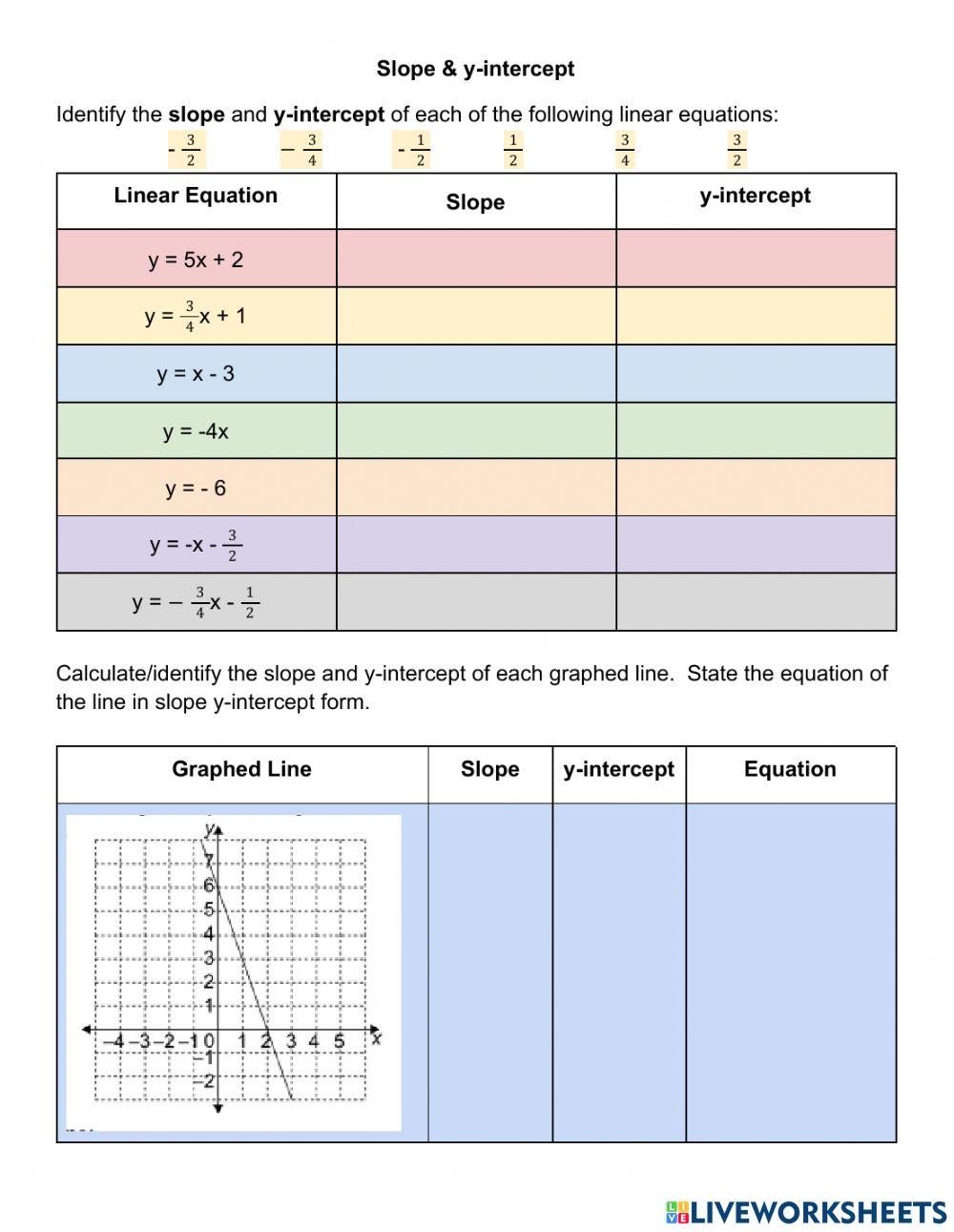
The slope-intercept form of a linear equation is given by y = mx + b, where m represents the slope of the line, and b is the y-intercept. This form directly provides the y-intercept as the constant term b. For instance, in the equation y = 2x + 3, the slope (m) is 2, and the y-intercept (b) is 3. This means the line crosses the y-axis at the point (0,3).
Method 1: Identifying the Y-Intercept from the Slope-Intercept Form
This method involves recognizing that the y-intercept is explicitly given in the slope-intercept form of the equation. If the equation is already in the form y = mx + b, then b is the y-intercept. This method is straightforward and requires no additional calculations if the equation is provided in slope-intercept form.
| Equation Form | Y-Intercept |
|---|---|
| y = 2x + 3 | 3 |
| y = -x - 2 | -2 |
| y = 4x + 1 | 1 |
Substituting X=0 into the Equation
The second method for finding the y-intercept involves substituting x=0 into the equation of the line, regardless of its form. This approach works because the y-intercept occurs at the point where x=0. By setting x to 0 and solving for y, one can find the y-intercept.
Method 2: Substituting X=0 into the Equation
To demonstrate this method, consider the equation y = 2x + 3. By substituting x=0 into the equation, we get y = 2(0) + 3, which simplifies to y = 3. Therefore, the y-intercept is 3. This method is universally applicable and can be used with equations in any form.
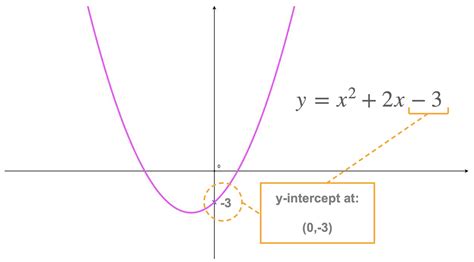
For example, given the equation y = x^2 + 2x + 1, substituting x=0 yields y = (0)^2 + 2(0) + 1 = 1. Thus, the y-intercept of this quadratic equation is 1.
Key Points
- The slope-intercept form of a linear equation, y = mx + b, directly provides the y-intercept as b.
- Substituting x=0 into any equation of a line will yield the y-intercept.
- Both methods are essential tools for understanding and analyzing linear equations and functions.
- The y-intercept is crucial for graphing lines and understanding their behavior.
- These methods apply to linear equations but can also be adapted for use with certain types of nonlinear equations.
In conclusion, finding the y-intercept of a line can be efficiently accomplished through two primary methods: recognizing the y-intercept in the slope-intercept form of the equation and substituting x=0 into the equation. Both approaches are fundamental techniques in algebra and geometry, offering insights into the properties and behaviors of lines and curves.
What is the slope-intercept form of a linear equation?
+The slope-intercept form is y = mx + b, where m is the slope and b is the y-intercept.
Why is substituting x=0 into an equation a method for finding the y-intercept?
+Substituting x=0 into an equation finds the y-intercept because the y-intercept is defined as the point where the line crosses the y-axis, which occurs when x=0.
Can these methods be used for nonlinear equations?
+While the primary focus is on linear equations, the method of substituting x=0 can be applied to certain types of nonlinear equations to find their y-intercepts. However, the slope-intercept form is specifically tailored for linear equations.