The concept of center of mass, also known as the center of gravity, is a fundamental principle in physics and engineering. It refers to the point where the entire mass of an object can be considered to be concentrated for the purpose of analyzing its motion. Understanding the center of mass is crucial in various fields, including mechanics, astronomy, and architecture, as it helps in predicting the behavior of objects under different forces and conditions. In this article, we will delve into the concept of center of mass, its significance, and how it can be calculated and applied in real-world scenarios.
Key Points
- The center of mass is the point where the weight of an object can be considered to act.
- It is a crucial concept in understanding the stability and balance of objects.
- The center of mass can be calculated using the formula: x_cm = (m1*x1 + m2*x2 +... + mn\*xn) / (m1 + m2 +... + mn), where x_cm is the x-coordinate of the center of mass, and m1, m2,..., mn are the masses of the individual parts of the object.
- The center of mass is not necessarily located within the physical boundaries of the object.
- Understanding the center of mass is essential in designing and analyzing systems, such as bridges, buildings, and mechanical systems.
What is Center of Mass?

The center of mass is the point where the entire mass of an object can be considered to be concentrated. It is the point where the weight of the object acts, and it is the reference point for analyzing the motion of the object. The center of mass is a geometric concept, and it is not necessarily located at the physical center of the object. For example, a ring has its center of mass at its geometric center, but a sphere has its center of mass at its geometric center only if it is homogeneous.
Calculating Center of Mass
The center of mass can be calculated using the formula: x_cm = (m1*x1 + m2*x2 +… + mn*xn) / (m1 + m2 +… + mn), where x_cm is the x-coordinate of the center of mass, and m1, m2,…, mn are the masses of the individual parts of the object. This formula can be applied to objects with multiple parts, such as a system of particles or a composite object. For example, if we have a system of two particles with masses m1 = 2 kg and m2 = 3 kg, and positions x1 = 1 m and x2 = 2 m, the x-coordinate of the center of mass is x_cm = (2*1 + 3*2) / (2 + 3) = 7⁄5 = 1.4 m.
| Object | Mass (kg) | Position (m) |
|---|---|---|
| Particle 1 | 2 | 1 |
| Particle 2 | 3 | 2 |
| Center of Mass | - | 1.4 |

Significance of Center of Mass
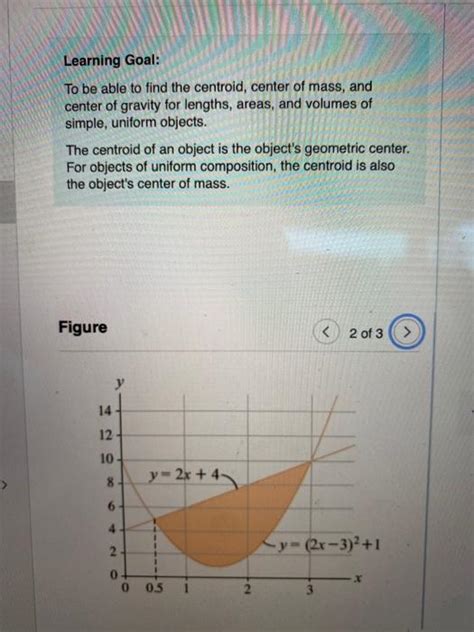
The center of mass is a critical concept in understanding the behavior of objects under different forces and conditions. It is essential in designing and analyzing systems, such as bridges, buildings, and mechanical systems. The center of mass helps in predicting the stability and balance of objects, and it is a key factor in determining the motion of objects under the influence of external forces. For example, a car with a low center of mass is more stable and less likely to roll over, while a car with a high center of mass is more prone to rolling over.
Real-World Applications
The concept of center of mass has numerous real-world applications. In engineering, it is used to design and analyze systems, such as bridges, buildings, and mechanical systems. In astronomy, it is used to predict the motion of celestial bodies, such as planets and stars. In sports, it is used to improve the performance of athletes, such as gymnasts and skaters. For example, a gymnast can improve their balance and stability by adjusting their center of mass during a routine.
What is the difference between center of mass and center of gravity?
+The center of mass and center of gravity are often used interchangeably, but they are not exactly the same. The center of mass is the point where the entire mass of an object can be considered to be concentrated, while the center of gravity is the point where the weight of the object acts. In a uniform gravitational field, the center of mass and center of gravity coincide, but in a non-uniform field, they can be different.
How is the center of mass used in engineering?
+The center of mass is used in engineering to design and analyze systems, such as bridges, buildings, and mechanical systems. It helps in predicting the stability and balance of objects, and it is a key factor in determining the motion of objects under the influence of external forces.
What are some common mistakes when calculating the center of mass?
+Common mistakes when calculating the center of mass include neglecting the distribution of mass within the object, using incorrect formulas, and failing to consider the effects of external forces. It is essential to carefully consider the mass distribution and the forces acting on the object to accurately calculate the center of mass.
In conclusion, the center of mass is a fundamental concept in physics and engineering, and it has numerous real-world applications. Understanding the center of mass is essential in designing and analyzing systems, predicting the stability and balance of objects, and determining the motion of objects under the influence of external forces. By carefully considering the mass distribution and the forces acting on an object, we can accurately calculate the center of mass and apply it to a wide range of problems and applications.



