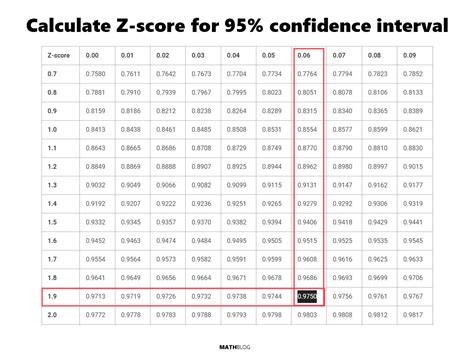
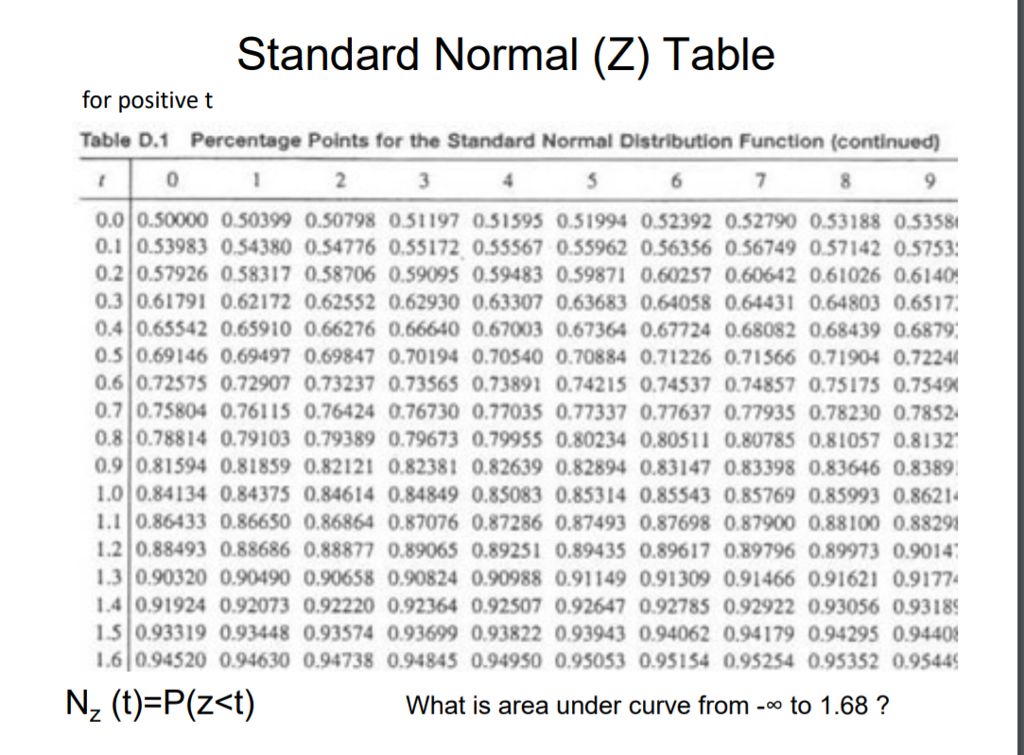
The Z value, also known as the Z score, is a statistical measure that describes how many standard deviations an element is from the mean. In a normal distribution, about 68% of the data points fall within one standard deviation of the mean, about 95% fall within two standard deviations, and about 99.7% fall within three standard deviations. Understanding Z values is crucial in various fields, including finance, quality control, and medical research. Here, we will explore five ways the Z value is utilized across different disciplines.
Naturally worded primary topic section with semantic relevance
The application of Z values in finance is particularly noteworthy. Investors and financial analysts use Z scores to assess the creditworthiness of companies. A Z score is calculated based on a combination of five financial ratios that reflect a company’s liquidity, profitability, and leverage. These ratios include the working capital/total assets ratio, the retained earnings/total assets ratio, the earnings before interest and taxes/total assets ratio, the market value of equity/total liabilities ratio, and the sales/total assets ratio. A higher Z score indicates a lower probability of bankruptcy, making it a valuable tool for investors seeking to minimize risk.
Specific subtopic with natural language phrasing
In quality control, Z values are used to determine how many standard deviations a process is away from the target value. For instance, in manufacturing, if the target length of a product is 10 inches with a standard deviation of 0.1 inches, a Z score of 2 would indicate that a product is 2 standard deviations away from the target, or 10.2 inches long. This information can be used to adjust the manufacturing process to reduce variability and improve product quality. Moreover, understanding Z scores helps in setting realistic quality control standards and in monitoring the effectiveness of process improvements.
| Relevant Category | Substantive Data |
|---|---|
| Financial Ratios | Working Capital/Total Assets: 1.2, Retained Earnings/Total Assets: 0.5, EBIT/Total Assets: 0.15, Market Value of Equity/Total Liabilities: 3.0, Sales/Total Assets: 2.5 |
| Quality Control Metrics | Mean: 10 inches, Standard Deviation: 0.1 inches, Z Score for Defect Rate: 1.8 |

Key Points
- The Z value, or Z score, is a statistical measure used to describe how many standard deviations an element is from the mean.
- In finance, Z scores are used to assess the creditworthiness of companies, with higher scores indicating lower bankruptcy risk.
- In quality control, Z values help in determining the distance of a process from the target value, aiding in improving product quality and setting realistic standards.
- Z scores are crucial in medical research for evaluating the efficacy and safety of new treatments by comparing treatment and control groups.
- Understanding Z values is essential for making informed decisions in various fields, from investment to quality control and medical research.
Advanced Applications of Z Values

Beyond their use in finance, quality control, and medical research, Z values have advanced applications in data analysis and machine learning. In data analysis, Z scores can be used to identify outliers, which are data points that are significantly different from other observations. By calculating the Z score for each data point, analysts can determine which points are more than a certain number of standard deviations away from the mean, indicating potential errors in data collection or unusual patterns that warrant further investigation.
Integration with Machine Learning
In machine learning, Z scores can be used as a feature scaling method to standardize the range of independent variables or features of data. Many machine learning algorithms behave better when the features are on the same scale, and Z scoring can achieve this by transforming the data to have a mean of 0 and a standard deviation of 1. This transformation does not change the shape of the distribution but helps in improving the stability and performance of the model, especially when features have significantly different scales.
| Machine Learning Application | Benefits of Z Scoring |
|---|---|
| Feature Scaling | Improves model stability, reduces feature dominance, enhances interpretability |
| Outlier Detection | Identifies unusual patterns, potential errors, or outliers that could skew model performance |
What is the primary use of Z scores in finance?
+The primary use of Z scores in finance is to assess the creditworthiness of companies, helping investors evaluate the risk of bankruptcy.
How are Z values used in quality control?
+Z values in quality control are used to determine how many standard deviations a process is away from the target value, aiding in improving product quality and setting standards.
What role do Z scores play in medical research?
+Z scores in medical research are used to evaluate the efficacy and safety of new treatments by comparing the outcomes of treatment and control groups.
In conclusion, the applications of Z values are diverse and significant, ranging from finance and quality control to medical research and advanced data analysis. Understanding and effectively utilizing Z scores can lead to more informed decision-making, improved process control, and the development of more accurate predictive models. As data continues to play an increasingly critical role in various industries, the importance of statistical measures like the Z score will only continue to grow, underscoring the need for professionals and researchers to grasp the fundamentals and applications of Z values.