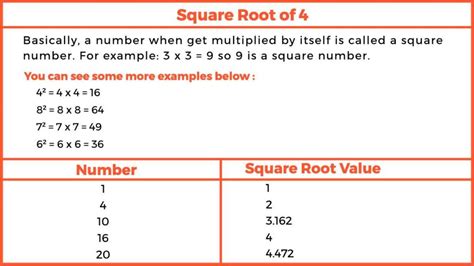
The square root of 4 is a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the number 4. In mathematical terms, it is expressed as √4. To find the square root of 4, one can use basic arithmetic operations or rely on mathematical properties of squares and square roots. The square root of a number is a value that, when squared, equals the original number. For example, the square root of 16 is 4 because 4 multiplied by 4 equals 16.
Calculating the Square Root of 4

The calculation of the square root of 4 is straightforward. Since 2 multiplied by 2 equals 4, the square root of 4 is 2. This can be represented as √4 = 2. The square root of a number can have two solutions, one positive and one negative, because both a positive number and its negative counterpart, when squared, give a positive result. Therefore, the square roots of 4 are 2 and -2, as both 2^2 and (-2)^2 equal 4.
Mathematical Representation
In mathematics, the square root of a number is denoted by the radical sign √. For the number 4, its square roots are represented as √4 = 2 and √4 = -2. The positive square root is sometimes denoted by the symbol +√, and the negative square root by -√, to differentiate between the two solutions. Understanding the concept of square roots is crucial in various mathematical disciplines, including algebra, geometry, and calculus, as it is used to solve equations, calculate distances, and determine the properties of geometric shapes.
| Number | Square Root |
|---|---|
| 4 | 2, -2 |
| 16 | 4, -4 |
| 25 | 5, -5 |
Key Points
- The square root of 4 is 2 and -2, as both 2^2 and (-2)^2 equal 4.
- The mathematical representation of the square root of a number is denoted by the radical sign √.
- Understanding square roots is crucial in various mathematical disciplines and has practical applications in science, engineering, and finance.
- The concept of square roots extends beyond positive numbers, with imaginary numbers representing the square roots of negative numbers.
- Calculating square roots is essential for solving equations, calculating distances, and determining the properties of geometric shapes.
The application of square roots in real-world scenarios is vast. In physics, the square root of the gravitational constant times the mass of two objects divided by the distance between their centers gives the gravitational force between them. In finance, square roots are used in the Black-Scholes model to calculate the value of options. The square root of time is a critical component in models that predict stock prices and volatility. The practical use of square roots demonstrates the pervasive nature of mathematical concepts in understanding and modeling the world around us.
Advanced Mathematical Concepts Involving Square Roots
Beyond the basic calculation of square roots, there are advanced mathematical concepts that involve the use of square roots. For instance, in algebra, solving quadratic equations often involves finding the square root of a number. The quadratic formula, which is used to solve equations of the form ax^2 + bx + c = 0, involves the square root of the discriminant (b^2 - 4ac). The discriminant determines the nature of the roots of the equation, whether they are real and distinct, real and equal, or complex.
Complex Numbers and Square Roots
In the realm of complex numbers, square roots take on a broader meaning. The square root of a negative number is represented by an imaginary unit, denoted as i, where i^2 = -1. For example, the square root of -4 is 2i, because (2i)^2 = 4i^2 = 4(-1) = -4. This extension of the real number system to include imaginary numbers allows for the square root of any number, positive or negative, to be defined.
The understanding and application of square roots, from basic arithmetic to advanced mathematical concepts, highlight the fundamental role this concept plays in mathematics and its applications. Whether in solving equations, modeling real-world phenomena, or exploring the properties of numbers, the square root is a powerful tool that underpins much of mathematical inquiry and discovery.
What is the square root of 4?
+The square root of 4 is 2 and -2, as both 2^2 and (-2)^2 equal 4.
How are square roots used in real-world applications?
+Square roots are used in various real-world applications, including physics to calculate forces, in finance to model stock prices and volatility, and in engineering to determine distances and properties of geometric shapes.
Can the square root of a negative number be calculated?
+Yes, the square root of a negative number can be calculated using complex numbers. For example, the square root of -4 is 2i, where i is the imaginary unit with the property that i^2 = -1.