Mathematics, often referred to as the language of numbers, encompasses a vast array of concepts, each with its unique terminology. The term "meaning" in math can be quite broad, as it can refer to the interpretation or significance of mathematical concepts, symbols, or expressions. Understanding the meaning behind mathematical terms is crucial for problem-solving, as it allows individuals to grasp the underlying principles and apply them appropriately. For instance, the concept of "variable" in algebra refers to a symbol that represents a value that can change, whereas in geometry, terms like "vertex" and "edge" have specific meanings related to the structure of shapes.
Delving deeper into mathematical terminology, we find that each branch of mathematics has its distinct vocabulary. In calculus, terms like "derivative" and "integral" have precise meanings related to rates of change and accumulation, respectively. Similarly, in number theory, terms such as "prime" and "composite" are used to describe the properties of integers. The meaning of these terms is not just about their definitions but also about how they are used within mathematical expressions and equations to convey specific mathematical ideas.
Key Points
- Understanding mathematical terminology is essential for effective communication and problem-solving in mathematics.
- The meaning of mathematical terms can vary significantly between different branches of mathematics.
- Mathematical expressions and equations rely on the precise meaning of terms to convey complex ideas and relationships.
- The interpretation of mathematical symbols and concepts is fundamental to applying mathematical principles in real-world applications.
- Continuous learning and review of mathematical terminology are necessary to maintain a deep understanding of mathematical concepts and their meanings.
Mathematical Symbols and Notations

Mathematical symbols and notations are another aspect where meaning plays a critical role. Symbols such as “+”, “-”, “×”, and “÷” have universally accepted meanings that are fundamental to arithmetic operations. However, as mathematics progresses to more advanced levels, symbols can take on different meanings. For example, the symbol “∫” represents integration in calculus, which is a concept entirely different from the simple arithmetic operations. The notation “f(x)” is used to denote a function of x, indicating a relationship between variables. Understanding the meaning behind these symbols and notations is crucial for interpreting and working with mathematical expressions.
Interpretation of Mathematical Expressions
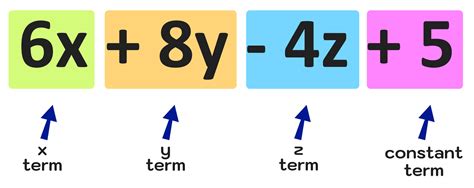
The interpretation of mathematical expressions involves understanding the meaning of both the symbols used and the context in which they are applied. For instance, the expression “2x + 5” in algebra refers to the sum of twice a variable x and the constant 5. In a different context, such as geometry, an expression might represent the dimensions of a shape or the relationship between different parts of a geometric figure. The ability to interpret these expressions correctly is based on a deep understanding of the meaning of mathematical terms and symbols.
| Mathematical Concept | Meaning |
|---|---|
| Variable | A symbol representing a value that can change. |
| Derivative | A measure of how a function changes as its input changes. |
| Integral | The accumulation of a quantity over a defined interval. |
| Prime Number | A positive integer greater than 1 that has no positive divisors other than 1 and itself. |
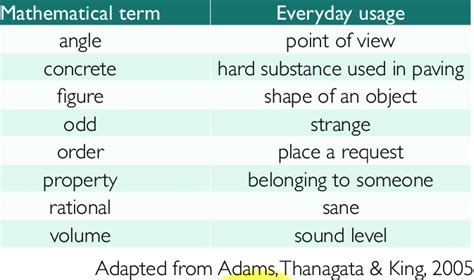
Applications of Mathematical Meaning

The application of mathematical meaning extends far beyond the classroom or theoretical discussions. In science and engineering, mathematical models are used to describe and predict the behavior of complex systems. The meaning of mathematical terms in these contexts is critical, as it directly affects the accuracy and reliability of the predictions made. For example, in physics, the equation E=mc^2 not only represents a relationship between energy (E) and mass (m) but also conveys a profound principle about the nature of energy and mass, with “c” representing the speed of light in a vacuum. This equation has far-reaching implications in nuclear physics and beyond, demonstrating how the meaning of mathematical terms can have significant real-world consequences.
In conclusion, the term "meaning" in mathematics encompasses a wide range of concepts, from the interpretation of symbols and notations to the understanding of complex mathematical principles. The depth and breadth of mathematical terminology reflect the complexity and beauty of mathematics itself, offering a precise language for describing the world and solving problems. As mathematics continues to evolve, understanding the meaning behind mathematical terms remains essential for advancing knowledge and applying mathematical principles in innovative ways.
What is the significance of understanding mathematical terminology?
+Understanding mathematical terminology is crucial for effective communication, problem-solving, and applying mathematical principles in various fields. It provides a foundation for interpreting mathematical expressions, understanding complex concepts, and making informed decisions based on mathematical models and predictions.
How does the meaning of mathematical terms vary across different branches of mathematics?
+The meaning of mathematical terms can vary significantly between different branches of mathematics. For example, terms like “derivative” and “integral” have specific meanings in calculus related to rates of change and accumulation, whereas in geometry, terms like “vertex” and “edge” refer to specific parts of geometric shapes. Understanding these variations is key to applying mathematical concepts correctly in different contexts.
What role does mathematical notation play in conveying mathematical meaning?
+Mathematical notation plays a critical role in conveying mathematical meaning by providing a precise and universally accepted way to represent mathematical concepts and relationships. Symbols and notations such as “+”, “-”, “×”, “÷”, “∫”, and “f(x)” have specific meanings that are fundamental to interpreting and working with mathematical expressions. The use of consistent notation helps in avoiding confusion and ensures that mathematical ideas are communicated clearly and accurately.