The tetrahedron, a polyhedron composed of four triangular faces, six straight edges, and four vertex corners, is one of the simplest and most fundamental shapes in geometry. Understanding its properties, including how to calculate its volume, is crucial in various fields such as mathematics, physics, engineering, and architecture. The volume of a tetrahedron can be calculated using a specific formula that involves the area of its base and its height. This article delves into the tetrahedron volume formula, exploring its derivation, application, and the nuances of calculating volumes for different types of tetrahedrons.
Key Points
- The tetrahedron volume formula is given by V = (1/3) * A * h, where A is the area of the base and h is the height from the base to the opposite vertex.
- The formula applies to all types of tetrahedrons, including regular and irregular ones, provided the base area and height are correctly identified.
- For a regular tetrahedron, the volume can also be calculated using the formula V = (a^3) / (6 * sqrt(2)), where a is the length of an edge.
- Understanding the volume of a tetrahedron is crucial in geometry, physics, and engineering for calculations involving space, density, and structural integrity.
- The derivation of the tetrahedron volume formula involves integrating the areas of cross-sections with respect to the height, similar to the volume calculations of other solids like pyramids.
Derivation of the Tetrahedron Volume Formula
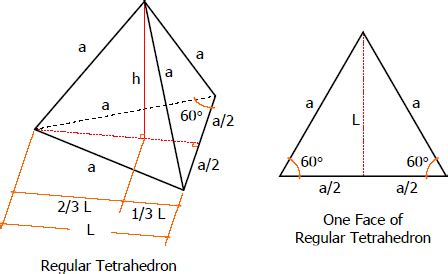
The tetrahedron volume formula is derived by considering the tetrahedron as a pyramid with a triangular base. The general formula for the volume of any pyramid is V = (1⁄3) * A * h, where A is the area of the base, and h is the perpendicular height from the base to the apex. For a tetrahedron, since one of its faces serves as the base, and the height is the perpendicular distance from the vertex opposite to this base to the plane containing the base, the same formula applies.
Calculating the Volume of a Regular Tetrahedron
A regular tetrahedron has all edges of equal length and all faces as equilateral triangles. The area of an equilateral triangle with side length a is given by A = (sqrt(3) / 4) * a^2. The height h of a regular tetrahedron can be found by dropping a perpendicular from the vertex opposite to the base to the center of the base, which intersects the base at its centroid, dividing the height into a 3:1 ratio from the vertex to the centroid and from the centroid to the base, respectively. The height h of a regular tetrahedron is h = a * sqrt(2⁄3). Substituting the area and height into the volume formula yields V = (a^3) / (6 * sqrt(2)) for a regular tetrahedron.
| Type of Tetrahedron | Volume Formula |
|---|---|
| General Tetrahedron | V = (1/3) * A * h |
| Regular Tetrahedron | V = (a^3) / (6 * sqrt(2)) |

Applications and Implications
Understanding and calculating the volume of a tetrahedron has numerous applications. In physics, the volume of an object is crucial for determining its density, which is defined as mass per unit volume. In engineering, knowing the volume of a tetrahedral structure helps in assessing its strength, stability, and the materials required for its construction. Furthermore, tetrahedral shapes are used in computer graphics for 3D modeling and in architecture for designing unique and stable structures.
Practical Considerations
In practical applications, especially involving irregular tetrahedrons, determining the exact area of the base and the height can be challenging. For complex shapes, breaking down the tetrahedron into simpler components or using numerical methods may be necessary. Additionally, in real-world scenarios, the material properties and the distribution of mass within the tetrahedron can affect its behavior under stress, necessitating a detailed analysis beyond simple volume calculations.
What is the formula for the volume of a regular tetrahedron?
+The volume V of a regular tetrahedron is given by V = (a^3) / (6 * sqrt(2)), where a is the length of an edge.
How do you calculate the height of a regular tetrahedron?
+The height h of a regular tetrahedron can be calculated as h = a * sqrt(2/3), where a is the length of an edge.
What is the general formula for the volume of any tetrahedron?
+The volume V of any tetrahedron is given by V = (1/3) * A * h, where A is the area of the base, and h is the height from the base to the opposite vertex.
In conclusion, the tetrahedron volume formula provides a fundamental tool for calculating the volume of one of the most basic yet versatile geometric shapes. Its applications span across various disciplines, from pure mathematics to practical engineering problems. Understanding and applying this formula requires a grasp of geometric principles, including the ability to calculate the area of triangular bases and the height of tetrahedrons, whether they are regular or irregular. As geometry continues to play a pivotal role in modern science and technology, the significance of the tetrahedron and its volume formula will only continue to grow.



