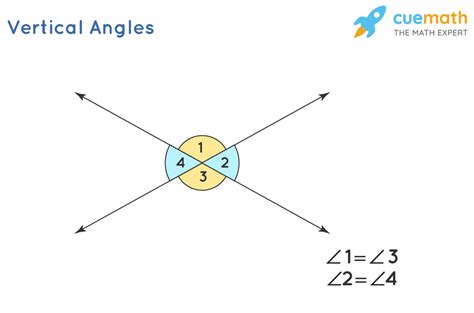
The Vertical Angle Theorem is a fundamental concept in geometry, stating that vertical angles, which are angles that share the same vertex and are formed by two intersecting lines, are always equal in measure. This theorem is crucial for solving various problems in geometry and trigonometry. Here, we will delve into the Vertical Angle Theorem, exploring its definition, application, and significance, while providing practical tips for mastering this concept.
Key Points
- Understanding the definition and application of the Vertical Angle Theorem is essential for geometry and trigonometry problem-solving.
- Recognizing the properties of vertical angles can simplify complex problems and provide a straightforward path to the solution.
- Applying the Vertical Angle Theorem in conjunction with other geometric principles can enhance problem-solving capabilities.
- Practice is key to mastering the Vertical Angle Theorem, as it helps in developing the ability to identify and apply the theorem in various scenarios.
- Integrating the Vertical Angle Theorem with real-world applications can make learning more engaging and relevant.
Definition and Application of the Vertical Angle Theorem
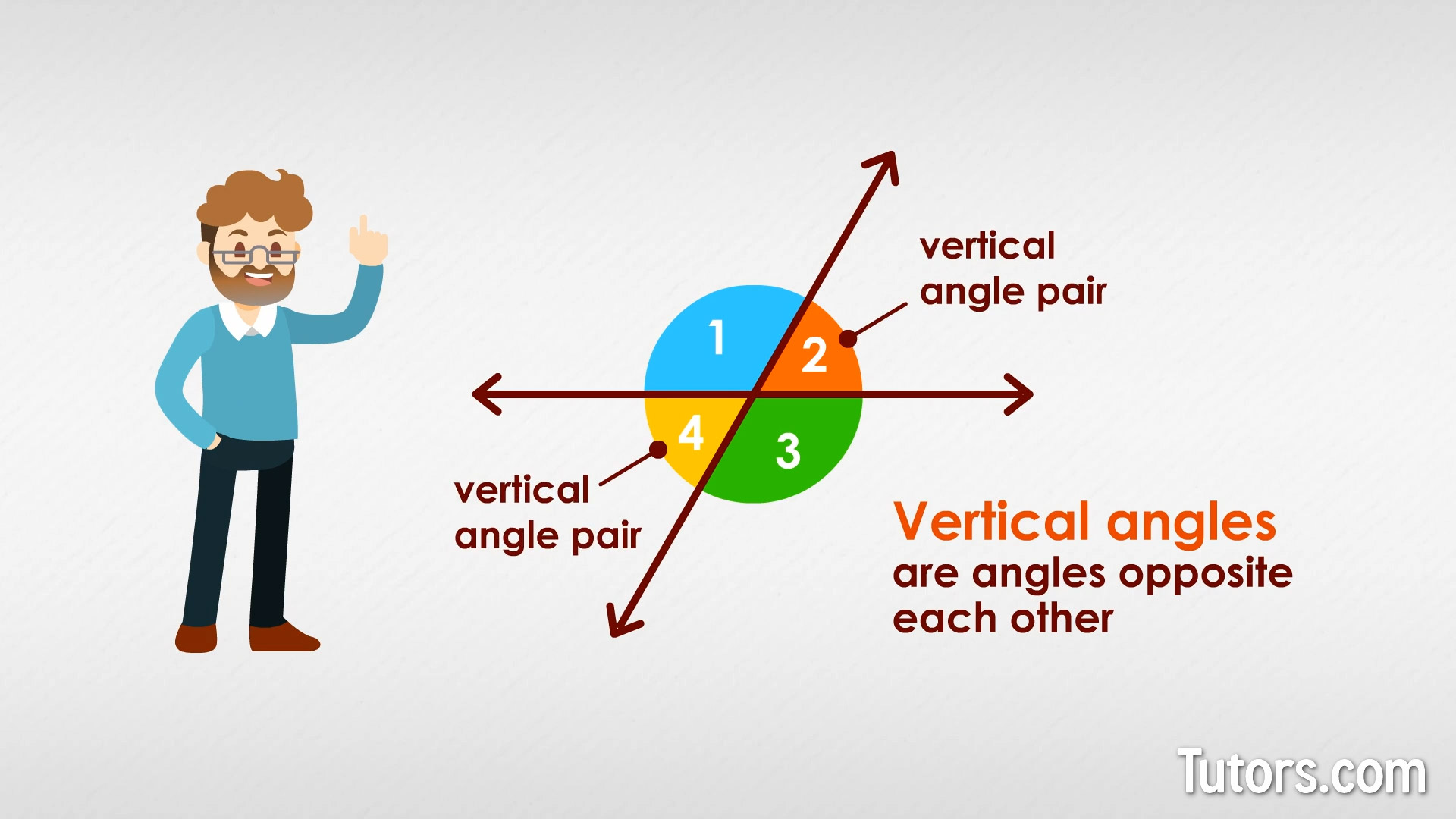
The Vertical Angle Theorem is defined as follows: If two angles are vertical angles, then they are congruent. This means that the measure of one angle is equal to the measure of the other angle. The application of this theorem is straightforward; whenever two angles are identified as vertical angles, their measures can be considered equal, which can significantly simplify geometric and trigonometric calculations.
Tip 1: Identify Vertical Angles Correctly
Identifying vertical angles correctly is the first step in applying the Vertical Angle Theorem. Vertical angles are formed by two intersecting lines, and they are always opposite each other. To identify vertical angles, look for the point of intersection of two lines and the angles that are directly across from each other at this intersection point.
Tip 2: Apply the Theorem in Various Geometric Contexts
The Vertical Angle Theorem can be applied in various geometric contexts, including but not limited to, solving for unknown angles in a diagram, proving angle relationships, and simplifying complex geometric configurations. By recognizing the applicability of the theorem in different contexts, one can enhance their geometric problem-solving skills.
Tip 3: Use the Theorem in Conjunction with Other Geometric Principles
The Vertical Angle Theorem is often used in conjunction with other geometric principles, such as the properties of complementary and supplementary angles, and the angle sum properties of triangles and polygons. By combining the Vertical Angle Theorem with these principles, one can tackle more complex geometric problems with ease.
Tip 4: Practice Applying the Theorem
Practice is essential for mastering the application of the Vertical Angle Theorem. Through consistent practice, one can develop the ability to quickly identify vertical angles and apply the theorem to simplify complex geometric configurations. Practice problems can range from straightforward applications of the theorem to more complex problems that require the integration of multiple geometric principles.
Tip 5: Explore Real-World Applications
Exploring the real-world applications of the Vertical Angle Theorem can make learning more engaging and relevant. The theorem has applications in architecture, engineering, and design, where understanding and applying geometric principles are crucial for creating structures and designs that are both aesthetically pleasing and functional. By exploring these applications, one can gain a deeper appreciation for the significance of the Vertical Angle Theorem and its role in solving real-world problems.
| Geometric Concept | Relevance to Vertical Angle Theorem |
|---|---|
| Complementary Angles | Understanding that vertical angles are equal can help in identifying complementary angles, which are angles whose measures add up to 90 degrees. |
| Supplementary Angles | Similarly, recognizing equal vertical angles can assist in identifying supplementary angles, which are angles whose measures add up to 180 degrees. |
| Triangle Angle Sum Property | The Vertical Angle Theorem can be used in conjunction with the triangle angle sum property (the sum of angles in a triangle is 180 degrees) to solve for unknown angles in a triangle. |
What is the primary application of the Vertical Angle Theorem?
+The primary application of the Vertical Angle Theorem is in solving geometric problems, particularly those involving intersecting lines and angles, by recognizing that vertical angles are equal in measure.
How does the Vertical Angle Theorem relate to other geometric principles?
+The Vertical Angle Theorem is often used in conjunction with other geometric principles, such as the properties of complementary and supplementary angles, and the angle sum properties of triangles and polygons, to solve complex geometric problems.
What is the significance of the Vertical Angle Theorem in real-world applications?
+The Vertical Angle Theorem has significant implications in real-world applications, including architecture, engineering, and design, where understanding geometric relationships and applying principles like the Vertical Angle Theorem are crucial for creating functional and aesthetically pleasing structures and designs.
In conclusion, the Vertical Angle Theorem is a foundational concept in geometry that offers a straightforward method for determining the equality of angles formed by intersecting lines. By understanding the definition, application, and significance of this theorem, and by practicing its application in various geometric contexts, individuals can develop a deeper understanding of geometric relationships and enhance their problem-solving capabilities. The integration of the Vertical Angle Theorem with other geometric principles and its application in real-world scenarios further underscores its importance and utility in the field of geometry.