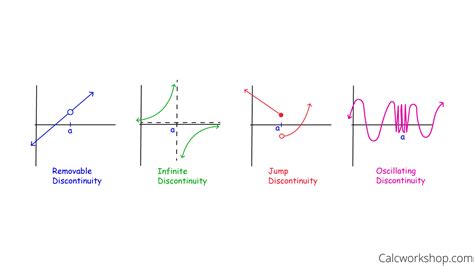
Discontinuity, a fundamental concept in various fields including mathematics, physics, and geology, refers to a point or set of points where a function, process, or phenomenon experiences a break or interruption in its continuity. This disruption can significantly affect the behavior, characteristics, or outcomes of the system under study. Understanding the different types of discontinuity is essential for analyzing, modeling, and predicting the behavior of complex systems across various disciplines. In this article, we will delve into the primary types of discontinuity, exploring their definitions, implications, and practical applications.
Key Points
- Discontinuity can be categorized into several types, including removable discontinuity, jump discontinuity, infinite discontinuity, and mixed discontinuity.
- Each type of discontinuity has distinct characteristics and implications for the function or system in question.
- Understanding discontinuity is crucial in mathematics, physics, and other fields for modeling real-world phenomena accurately.
- Practical applications of discontinuity analysis include electrical engineering, materials science, and geophysics.
- The concept of discontinuity also plays a significant role in economics, finance, and social sciences, particularly in modeling abrupt changes or crises.
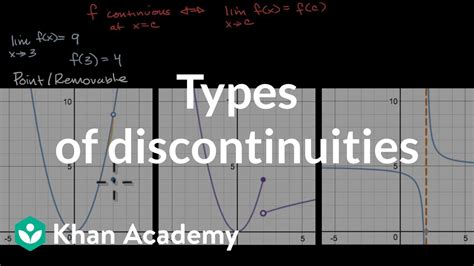
Removable Discontinuity

A removable discontinuity occurs when a function is not defined at a specific point, but the limit of the function as it approaches that point exists. This type of discontinuity can often be “removed” by redefining the function at the problematic point to match the limit. Removable discontinuities are also known as “holes” in the graph of the function because they appear as isolated points where the function is not defined, but the surrounding behavior of the function is consistent.
Characteristics and Examples
Removable discontinuities are typically found in rational functions where there is a factor in the denominator that can be canceled out by a corresponding factor in the numerator, except at the point where the denominator equals zero. For instance, the function f(x) = (x^2 - 4) / (x - 2) has a removable discontinuity at x = 2 because the factor (x - 2) can be canceled from both the numerator and the denominator, leaving f(x) = x + 2 for x ≠ 2. This simplification shows that the limit of f(x) as x approaches 2 exists and equals 4, even though f(2) is technically undefined.
| Type of Discontinuity | Description | Example |
|---|---|---|
| Removable | Limit exists, but function is undefined at the point | f(x) = (x^2 - 4) / (x - 2) at x = 2 |
| Jump | Limit does not exist due to differing one-sided limits | f(x) = 0 for x < 0, f(x) = 1 for x ≥ 0 |
| Infinite | Limit is infinity, often due to vertical asymptotes | f(x) = 1 / x at x = 0 |
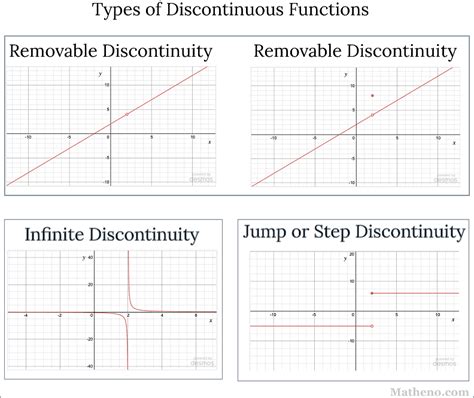
Jump Discontinuity
A jump discontinuity, also known as a discontinuity of the first kind, occurs when the one-sided limits of a function at a point exist but are not equal. This results in a “jump” in the graph of the function at that point. The function value at the point of discontinuity may or may not be defined, but the key characteristic is the difference between the left and right limits.
Implications and Examples
Jump discontinuities are common in piecewise functions where different rules apply on either side of a boundary point. For example, the function f(x) = 0 for x < 0 and f(x) = 1 for x ≥ 0 has a jump discontinuity at x = 0 because the left limit is 0 and the right limit is 1, and there is no value of f(0) that can make the function continuous at x = 0.
Infinite Discontinuity
An infinite discontinuity, or discontinuity of the second kind, occurs when a function approaches positive or negative infinity as it gets closer to a certain point. This is often due to vertical asymptotes in rational functions where the denominator approaches zero, causing the function value to become infinitely large.
Characteristics and Examples
The function f(x) = 1 / x exhibits an infinite discontinuity at x = 0 because as x approaches 0 from the right, f(x) approaches positive infinity, and as x approaches 0 from the left, f(x) approaches negative infinity. This behavior indicates that the function has no finite limit at x = 0 and thus is not continuous there.
Mixed Discontinuity
A mixed discontinuity combines elements of jump and infinite discontinuities, where one side of the limit approaches a finite value and the other side approaches infinity. This type of discontinuity reflects a more complex behavior where the function’s approach to the point of discontinuity is fundamentally different on each side.
Implications and Practical Applications
Understanding the types of discontinuity is not only crucial for theoretical mathematics but also has significant implications for practical applications. In electrical engineering, for instance, discontinuities in circuit functions can represent switches or sudden changes in the circuit’s configuration. In materials science, the study of discontinuities in material properties can help understand fracture mechanics and failure points. Furthermore, in geophysics, analyzing discontinuities in seismic data is essential for understanding the structure of the Earth’s crust.
What are the primary types of discontinuity?
+The primary types of discontinuity include removable discontinuity, jump discontinuity, infinite discontinuity, and mixed discontinuity. Each type has distinct characteristics and implications for the function or system under study.
Why is understanding discontinuity important in practical applications?
+Understanding discontinuity is crucial for modeling and predicting the behavior of complex systems accurately. Discontinuities can represent significant changes or failures in systems, such as electrical circuits, material properties, or geological structures, making their analysis essential for design, safety, and predictive purposes.
How does the concept of discontinuity apply to fields beyond mathematics and physics?
+The concept of discontinuity is also significant in economics, finance, and social sciences, particularly in modeling sudden changes, crises, or phase transitions. For example, economic models may include discontinuities to represent policy changes, market crashes, or other abrupt events that significantly impact economic behavior.
In conclusion, discontinuity is a multifaceted concept that plays a vital role in understanding and analyzing complex systems across various disciplines. By recognizing and categorizing the different types of discontinuity, researchers and practitioners can better model, predict, and manage the behavior of these systems, leading to advancements in fields ranging from mathematics and physics to economics and geophysics. The nuanced understanding of discontinuity, as explored in this article, underscores the importance of detailed analysis and the consideration of potential discontinuities in any system or phenomenon under study.