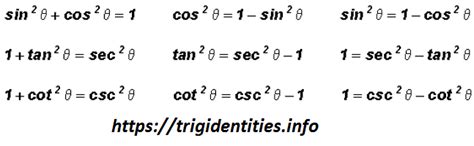Trigonometric Pythagorean identities are fundamental concepts in trigonometry, providing a crucial link between the sine and cosine functions. These identities are derived from the Pythagorean theorem and are essential in various mathematical and scientific applications. The most basic Pythagorean identity is sin²(x) + cos²(x) = 1, which holds true for all angles x. This identity can be proven using the unit circle, where the sine and cosine of an angle are defined as the ratios of the lengths of the sides of a right triangle.
In this context, understanding the unit circle is vital. It is a circle with a radius of 1, centered at the origin of a coordinate plane. The sine of an angle in a right triangle is the ratio of the length of the side opposite the angle to the hypotenuse (the side opposite the right angle), while the cosine is the ratio of the length of the side adjacent to the angle to the hypotenuse. Using these definitions and the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides, we can derive the Pythagorean identity.
Key Points
- The Pythagorean identity sin²(x) + cos²(x) = 1 is a fundamental concept in trigonometry.
- This identity is derived from the Pythagorean theorem and the definitions of sine and cosine in a right triangle.
- Understanding the unit circle is crucial for comprehending the Pythagorean identities.
- These identities have numerous applications in mathematics, physics, engineering, and other sciences.
- Derivations of the Pythagorean identities can vary, including geometric and algebraic approaches.
Derivation and Applications
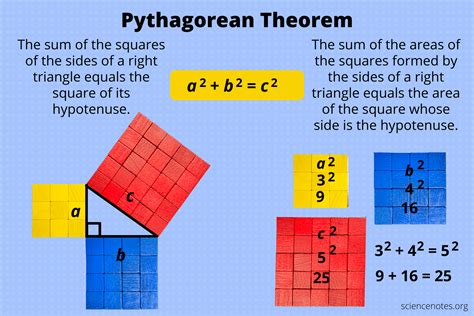
The derivation of the Pythagorean identity can be approached through geometric and algebraic methods. Geometrically, it can be shown using the unit circle, where the coordinates of a point on the circle can be used to represent the cosine and sine of an angle. Algebraically, it can be derived by considering the equations of the sine and cosine functions and applying the Pythagorean theorem.
These identities have extensive applications in various fields. In physics, they are used to describe the motion of objects in terms of their components along different axes. In engineering, they are crucial in the design and analysis of structures, mechanisms, and electronic circuits. In mathematics, they are essential for more advanced trigonometric identities and in the study of periodic functions.
Other Pythagorean Identities
Besides the basic identity, there are other Pythagorean identities that relate the sine and cosine functions. These include 1 + tan²(x) = sec²(x) and 1 + cot²(x) = csc²(x), which can be derived from the basic identity by using the definitions of the tangent, secant, cotangent, and cosecant functions. The tangent of an angle is the ratio of the sine to the cosine, the secant is the reciprocal of the cosine, the cotangent is the reciprocal of the tangent, and the cosecant is the reciprocal of the sine.
| Trigonometric Function | Definition |
|---|---|
| Sine (sin) | Opposite side / Hypotenuse |
| Cosine (cos) | Adjacent side / Hypotenuse |
| Tangent (tan) | Opposite side / Adjacent side |
| Secant (sec) | Hypotenuse / Adjacent side |
| Cotangent (cot) | Adjacent side / Opposite side |
| Cosecant (csc) | Hypotenuse / Opposite side |

Problem-Solving Strategies

When applying Pythagorean identities in problem-solving, it’s essential to first identify the given information and what needs to be found. Often, the goal is to express a trigonometric expression in terms of a single function or to simplify a complex expression. Utilizing the Pythagorean identities can help in simplifying expressions, solving equations, and proving other trigonometric identities.
A critical strategy is to recognize when to use each identity. For instance, if an expression involves both sine and cosine, the basic Pythagorean identity might be useful. If the expression involves tangent and secant, the identity 1 + tan²(x) = sec²(x) could be more appropriate. Additionally, understanding the relationships between the trigonometric functions and their reciprocal identities can facilitate the simplification process.
Advanced Applications and Extensions
Beyond the foundational aspects, trigonometric Pythagorean identities play a role in more advanced mathematical and scientific applications. In calculus, they are used in the derivation of differentiation rules for trigonometric functions. In complex analysis, these identities are essential for understanding the properties of complex trigonometric functions. Furthermore, in physics and engineering, they are crucial in the study of wave phenomena, including sound waves and light waves, where trigonometric functions describe the oscillatory behavior of these waves.
What is the primary use of the Pythagorean identity in trigonometry?
+The primary use of the Pythagorean identity is to express a trigonometric expression in terms of a single trigonometric function, facilitating simplification and problem-solving in various trigonometric contexts.
How are Pythagorean identities derived?
+Pythagorean identities can be derived geometrically using the unit circle or algebraically by manipulating the definitions of sine, cosine, and other trigonometric functions in the context of the Pythagorean theorem.
What are some common applications of trigonometric Pythagorean identities?
+Common applications include simplifying trigonometric expressions, solving trigonometric equations, and describing periodic phenomena in physics and engineering, among others.
In conclusion, trigonometric Pythagorean identities are cornerstone concepts in mathematics and science, offering powerful tools for simplification, problem-solving, and analysis. Their derivation, applications, and extensions underscore the interconnectedness of mathematical principles and their profound impact on our understanding of the world.