The Taylor series, named after James Gregory and Brook Taylor, is a powerful mathematical tool used to approximate functions near a point. This concept is fundamental in calculus and has numerous applications in various fields, including physics, engineering, and computer science. Understanding the Taylor series is crucial for any student or professional working with mathematical models. Here are five tips to help you better comprehend and work with the Taylor series:
Key Points
- Understand the general form of the Taylor series and its application to common functions.
- Learn how to derive the Taylor series for a given function, focusing on the first few terms for approximation.
- Recognize the importance of the remainder term in assessing the accuracy of the approximation.
- Familiarize yourself with the geometric series as a basic example of a Taylor series expansion.
- Apply the Taylor series in solving problems and modeling real-world phenomena, considering the limitations and potential for convergence.
Understanding the Taylor Series

The Taylor series of a function f(x) around a point a is given by the infinite series: f(x) = f(a) + f’(a)(x-a) + f”(a)(x-a)^2⁄2! + f”‘(a)(x-a)^3⁄3! +…. This series represents the function as an infinite sum of terms that are expressed in terms of the values of the function’s derivatives at the point a. For many functions, especially those that are infinitely differentiable, the Taylor series provides a way to approximate the function near a with arbitrary precision by summing a sufficient number of terms.
Deriving the Taylor Series for Common Functions
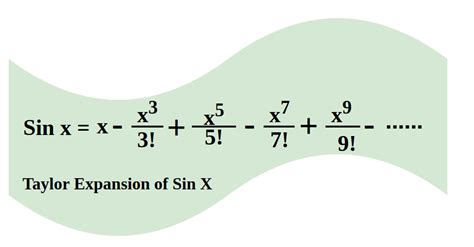
A critical skill in working with Taylor series is the ability to derive the series for a given function. For example, the Taylor series for the exponential function e^x around x=0 is 1 + x + x^2⁄2! + x^3⁄3! +…. This series can be derived by computing the derivatives of e^x at x=0 and plugging these values into the Taylor series formula. Similarly, the Taylor series for sin(x) and cos(x) around x=0 can be derived, resulting in sin(x) = x - x^3⁄3! + x^5⁄5! -… and cos(x) = 1 - x^2⁄2! + x^4⁄4! -…. These series are crucial in trigonometry and are used extensively in physics and engineering.
| Function | Taylor Series Expansion |
|---|---|
| Exp(x) | 1 + x + x^2/2! + x^3/3! +... |
| Sin(x) | x - x^3/3! + x^5/5! -... |
| Cos(x) | 1 - x^2/2! + x^4/4! -... |
Applications and Limitations

The Taylor series has numerous applications, from solving differential equations to modeling complex systems. However, it’s also important to understand its limitations. The series may not converge for all values of x, and even when it does, the rate of convergence can be slow, requiring a large number of terms for a good approximation. The remainder term of the Taylor series provides a bound on the error of the approximation, which is essential for assessing the accuracy of the result.
Geometric Series as a Taylor Series Expansion
A simple yet instructive example of a Taylor series is the geometric series. The function 1/(1-x) can be expanded as 1 + x + x^2 + x^3 +… for |x| < 1. This series is a Taylor series expansion of the function around x=0 and illustrates how a function can be represented as an infinite sum of terms. The geometric series is a basic example but demonstrates the power of the Taylor series in approximating functions.
In conclusion, the Taylor series is a versatile tool in mathematics and science, offering a way to approximate functions, solve equations, and model real-world phenomena. By understanding how to derive and apply Taylor series, and being aware of their limitations, you can leverage this powerful mathematical concept to tackle complex problems in a wide range of fields.
What is the main application of the Taylor series in mathematics and science?
+The Taylor series is primarily used for approximating functions near a point, solving differential equations, and modeling complex systems. It provides a way to represent a function as an infinite sum of terms, which can be used to approximate the function with arbitrary precision.
How do you determine the convergence of a Taylor series?
+The convergence of a Taylor series can be determined by examining the remainder term or using convergence tests such as the ratio test or root test. The series converges if the limit of the remainder term approaches zero as the number of terms approaches infinity.
What is the significance of the geometric series in the context of Taylor series expansions?
+The geometric series is a basic example of a Taylor series expansion, illustrating how a function can be represented as an infinite sum of terms. It demonstrates the power of the Taylor series in approximating functions and is a fundamental building block for more complex series expansions.



