The Taylor polynomial is a fundamental concept in calculus, used to approximate functions at a given point. It is a powerful tool for understanding the behavior of functions and has numerous applications in mathematics, physics, and engineering. In this article, we will explore five ways to utilize Taylor polynomials, highlighting their importance and versatility in mathematical analysis.
Key Points
- Taylor polynomials provide a way to approximate functions at a given point, enabling the analysis of function behavior.
- The Taylor series expansion can be used to derive important mathematical constants, such as e and π.
- Taylor polynomials are essential in numerical analysis, allowing for the approximation of complex functions and the solution of differential equations.
- The remainder theorem provides a way to estimate the error in the approximation, ensuring the accuracy of the results.
- Taylor polynomials have numerous applications in physics and engineering, including the modeling of population growth, electrical circuits, and mechanical systems.
Introduction to Taylor Polynomials
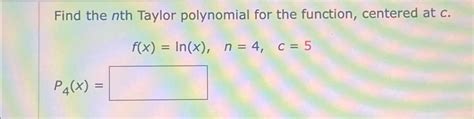
A Taylor polynomial is a polynomial approximation of a function at a given point. It is defined as the sum of the terms of the Taylor series, which are determined by the function’s derivatives at the point of expansion. The Taylor polynomial of degree n is given by the formula:
T_n(x) = f(a) + f’(a)(x-a) + f”(a)(x-a)^2⁄2! +… + f^(n)(a)(x-a)^n/n!
This formula provides a way to approximate the function f(x) at the point x, using the values of the function and its derivatives at the point a.
Taylor Series Expansion
The Taylor series expansion is a powerful tool for deriving important mathematical constants. For example, the Taylor series expansion of the exponential function e^x is given by:
e^x = 1 + x + x^2⁄2! + x^3⁄3! +…
This expansion can be used to derive the value of e, which is approximately 2.71828. Similarly, the Taylor series expansion of the trigonometric functions sin(x) and cos(x) can be used to derive the values of π and other important mathematical constants.
Numerical Analysis and Approximation

Taylor polynomials are essential in numerical analysis, allowing for the approximation of complex functions and the solution of differential equations. The Taylor polynomial can be used to approximate the solution of a differential equation, by using the initial conditions and the differential equation itself to determine the coefficients of the polynomial. This method is known as the Taylor series method, and it is widely used in numerical analysis and scientific computing.
Remainder Theorem and Error Estimation
The remainder theorem provides a way to estimate the error in the approximation, ensuring the accuracy of the results. The remainder theorem states that the error in the approximation is bounded by the remainder term, which is given by:
R_n(x) = f^(n+1)©(x-a)^(n+1)/(n+1)!
where c is a point between a and x. This theorem provides a way to estimate the error in the approximation, and to determine the degree of the polynomial required to achieve a given level of accuracy.
Applications in Physics and Engineering
Taylor polynomials have numerous applications in physics and engineering, including the modeling of population growth, electrical circuits, and mechanical systems. The Taylor polynomial can be used to model the behavior of complex systems, by using the initial conditions and the differential equations that govern the system to determine the coefficients of the polynomial. This method is widely used in physics and engineering, and it has numerous applications in fields such as mechanics, electromagnetism, and thermodynamics.
| Application | Description |
|---|---|
| Population Growth | The Taylor polynomial can be used to model the growth of populations, by using the initial population and the growth rate to determine the coefficients of the polynomial. |
| Electrical Circuits | The Taylor polynomial can be used to model the behavior of electrical circuits, by using the initial conditions and the differential equations that govern the circuit to determine the coefficients of the polynomial. |
| Mechanical Systems | The Taylor polynomial can be used to model the behavior of mechanical systems, by using the initial conditions and the differential equations that govern the system to determine the coefficients of the polynomial. |

What is the Taylor polynomial?
+The Taylor polynomial is a polynomial approximation of a function at a given point, defined as the sum of the terms of the Taylor series.
What is the Taylor series expansion?
+The Taylor series expansion is a powerful tool for deriving important mathematical constants, such as e and π, by using the Taylor series of the exponential and trigonometric functions.
What is the remainder theorem?
+The remainder theorem provides a way to estimate the error in the approximation, by bounding the error by the remainder term.