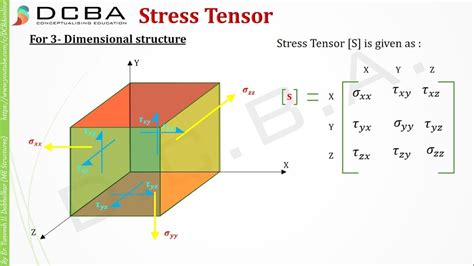
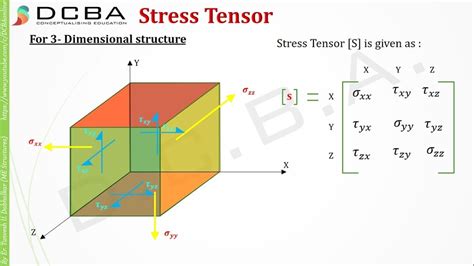
The stress tensor is a fundamental concept in the field of continuum mechanics, playing a crucial role in the description of the internal forces that arise within a material due to external loads. It is a mathematical representation that quantifies the normal and shear stresses acting on a small cube of material, providing a comprehensive understanding of the stress state at a point. The stress tensor is denoted by the symbol σ and is typically represented as a 3x3 matrix, with its components representing the normal and shear stresses in the x, y, and z directions.
Mathematically, the stress tensor can be expressed as:
σ = σxx ex ex + σyy ey ey + σzz ez ez + τxy ex ey + τyx ey ex + τxz ex ez + τzx ez ex + τyz ey ez + τzy ez ey
where ex, ey, and ez are the unit vectors in the x, y, and z directions, respectively. The diagonal components of the stress tensor (σxx, σyy, and σzz) represent the normal stresses, while the off-diagonal components (τxy, τyx, τxz, τzx, τyz, and τzy) represent the shear stresses.
Naturally worded primary topic section with semantic relevance
The stress tensor is used to describe the state of stress at a point in a material, which is essential in understanding the behavior of the material under various types of loading. The stress tensor is a powerful tool in the analysis of complex stress states, as it provides a comprehensive understanding of the normal and shear stresses acting on a material. In the field of engineering, the stress tensor is used to design and analyze structures, such as bridges, buildings, and mechanical components, to ensure that they can withstand various types of loading without failing.
The stress tensor is also used in the field of materials science to understand the behavior of materials under different types of loading. For example, the stress tensor can be used to analyze the stress state of a material under uniaxial tension, bending, or torsion. By understanding the stress state of a material, researchers and engineers can design new materials with improved properties, such as strength, toughness, and ductility.
Specific subtopic with natural language phrasing
The stress tensor can be used to calculate various stress invariants, which are scalar quantities that provide a comprehensive understanding of the stress state at a point. The first stress invariant (I1) is calculated as the sum of the diagonal components of the stress tensor, while the second stress invariant (I2) is calculated as the sum of the products of the diagonal components. The third stress invariant (I3) is calculated as the determinant of the stress tensor.
These stress invariants are used in various engineering applications, such as the design of pressure vessels and pipelines. For example, the first stress invariant (I1) is used to calculate the hydrostatic stress of a material, which is essential in understanding the behavior of materials under high-pressure conditions.
| Stress Invariant | Formula |
|---|---|
| First Stress Invariant (I1) | σxx + σyy + σzz |
| Second Stress Invariant (I2) | σxx σyy + σxx σzz + σyy σzz |
| Third Stress Invariant (I3) | σxx σyy σzz + 2 τxy τxz τyz |

Key Points
- The stress tensor is a 3x3 matrix that represents the normal and shear stresses acting on a material.
- The stress tensor is used to describe the state of stress at a point in a material, which is essential in understanding the behavior of the material under various types of loading.
- The stress tensor can be used to calculate various stress invariants, which provide a comprehensive understanding of the stress state at a point.
- The stress tensor is used in various engineering applications, such as the design of pressure vessels and pipelines.
- The stress tensor is a powerful tool in the analysis of complex stress states, and its applications are diverse and widespread.
Applications of the Stress Tensor
The stress tensor has numerous applications in various fields of engineering and materials science. One of the most significant applications of the stress tensor is in the design and analysis of structural components, such as beams, columns, and plates. The stress tensor is used to calculate the stresses and strains in these components, which is essential in understanding their behavior under various types of loading.
Another significant application of the stress tensor is in the field of materials science. The stress tensor is used to understand the behavior of materials under different types of loading, such as tension, compression, and shear. By understanding the stress state of a material, researchers and engineers can design new materials with improved properties, such as strength, toughness, and ductility.
Stress Tensor in Engineering Applications
The stress tensor is used in various engineering applications, such as the design of pressure vessels and pipelines. The stress tensor is used to calculate the stresses and strains in these components, which is essential in understanding their behavior under various types of loading. For example, the stress tensor is used to calculate the hoop stress and axial stress in a pipe, which is essential in understanding its behavior under internal pressure.
The stress tensor is also used in the field of mechanical engineering to design and analyze mechanical components, such as gears, bearings, and shafts. The stress tensor is used to calculate the stresses and strains in these components, which is essential in understanding their behavior under various types of loading.
What is the stress tensor?
+The stress tensor is a 3x3 matrix that represents the normal and shear stresses acting on a material.
What are the applications of the stress tensor?
+The stress tensor has numerous applications in various fields of engineering and materials science, including the design and analysis of structural components, materials science, and mechanical engineering.
How is the stress tensor used in engineering applications?
+The stress tensor is used to calculate the stresses and strains in various components, such as pressure vessels, pipelines, and mechanical components, which is essential in understanding their behavior under various types of loading.