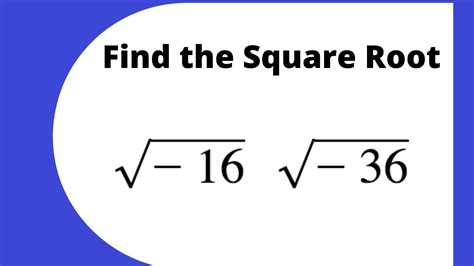The concept of "i" is a fundamental element in mathematics, particularly in the realm of complex numbers. It represents the imaginary unit, which is defined as the square root of -1. Understanding "i" is crucial for advancing in various mathematical and scientific disciplines. In this article, we will delve into five ways to comprehend the concept of "i" and its significance in different contexts.
Key Points
- The imaginary unit "i" is defined as the square root of -1.
- Complex numbers, which include "i", are essential in mathematics, physics, and engineering.
- Visualizing "i" on the complex plane helps in understanding its properties and applications.
- "i" plays a critical role in algebra, particularly in solving quadratic equations and polynomial factorization.
- The concept of "i" has numerous practical applications in fields like electrical engineering, signal processing, and cryptography.
Introduction to Complex Numbers and “i”

Complex numbers are an extension of the real number system, and they include a real part and an imaginary part. The imaginary part is represented by “i”, which satisfies the equation i^2 = -1. This concept may seem abstract at first, but it has far-reaching implications in various mathematical and scientific disciplines. To grasp the concept of “i”, it is essential to understand the complex plane, where complex numbers are represented as points on a two-dimensional plane.
Visualizing “i” on the Complex Plane
The complex plane is a graphical representation of complex numbers, where the x-axis represents the real part and the y-axis represents the imaginary part. The point (0,1) on the complex plane corresponds to the imaginary unit “i”. Visualizing “i” on the complex plane helps in understanding its properties, such as rotation and scaling, which are crucial in various applications. For instance, multiplying a complex number by “i” corresponds to a 90-degree rotation in the counterclockwise direction.
| Complex Number Operation | Result |
|---|---|
| i^2 | -1 |
| i^3 | -i |
| i^4 | 1 |

Algebraic Applications of “i”

The concept of “i” plays a critical role in algebra, particularly in solving quadratic equations and polynomial factorization. For example, the quadratic formula, which is used to solve quadratic equations, involves “i” when the discriminant is negative. Additionally, “i” is used in polynomial factorization, where it helps to factorize polynomials into simpler expressions. Understanding “i” is essential for advancing in algebra and other mathematical disciplines.
Practical Applications of “i”
The concept of “i” has numerous practical applications in fields like electrical engineering, signal processing, and cryptography. In electrical engineering, “i” is used to represent the impedance of circuits, which is crucial for designing and analyzing electrical systems. In signal processing, “i” is used to represent the frequency domain, which is essential for filtering and analyzing signals. In cryptography, “i” is used in encryption algorithms, such as the RSA algorithm, which relies on the properties of complex numbers to secure data.
Conclusion and Future Directions
In conclusion, the concept of “i” is a fundamental element in mathematics, and understanding it is crucial for advancing in various mathematical and scientific disciplines. The five ways to comprehend “i” presented in this article, including visualizing “i” on the complex plane, algebraic applications, and practical applications, provide a comprehensive understanding of this complex concept. As research continues to advance, the concept of “i” will remain a vital component of mathematical and scientific discoveries.
What is the definition of "i" in mathematics?
+The imaginary unit "i" is defined as the square root of -1, which satisfies the equation i^2 = -1.
What are the practical applications of "i" in electrical engineering?
+In electrical engineering, "i" is used to represent the impedance of circuits, which is crucial for designing and analyzing electrical systems.
How is "i" used in cryptography?
+In cryptography, "i" is used in encryption algorithms, such as the RSA algorithm, which relies on the properties of complex numbers to secure data.
Meta Description: Discover the five ways to understand the concept of “i” and its significance in mathematics, including its definition, algebraic applications, and practical uses in electrical engineering and cryptography.