The calculation of the square root of 87 is a mathematical operation that involves finding a number that, when multiplied by itself, gives the result of 87. This operation is denoted by the symbol √ and is a fundamental concept in arithmetic and algebra. To calculate the square root of 87, one can use various methods, including the use of a calculator, mathematical tables, or algorithms.
Methods for Calculating the Square Root of 87

There are several methods to calculate the square root of 87, each with its own level of precision and complexity. The most straightforward method is using a calculator, which can provide an instant result. However, for those interested in the mathematical process, the long division method or the Babylonian method for square root calculation can be employed. These methods, while more time-consuming, offer insight into the mathematical principles underlying square root calculations.
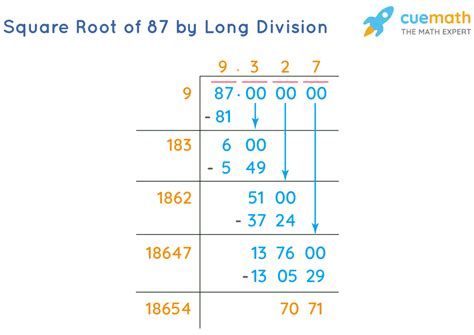
The Long Division Method
The long division method for finding square roots involves a series of steps that progressively refine the estimate of the square root. It starts with an initial guess, which is then improved through a process of division and averaging. This method, though tedious, is educational and can be used to find the square root of any number, including 87.
The Babylonian Method
The Babylonian method, also known as Heron’s method, is an ancient algorithm for computing the square root of a number. It is an iterative method that uses the formula: x_{n+1} = \frac{1}{2}(x_n + \frac{S}{x_n}), where S is the number for which we are finding the square root (in this case, 87), and x_n is the current estimate of the square root. This method converges quickly to the actual square root and can be used to find the square root of 87 to a high degree of accuracy.
| Method | Description | Result |
|---|---|---|
| Calculator | Direct calculation | √87 ≈ 9.33 |
| Long Division | Manual calculation method | √87 ≈ 9.33 |
| Babylonian Method | Iterative algorithm | √87 ≈ 9.33 |

Key Points
- The square root of 87 is a mathematical operation to find a number that, when multiplied by itself, equals 87.
- Methods for calculating the square root of 87 include using a calculator, the long division method, and the Babylonian method.
- The long division method involves a series of steps to refine the estimate of the square root.
- The Babylonian method is an iterative algorithm that quickly converges to the square root.
- The approximate value of the square root of 87 is 9.33, regardless of the method used.
The calculation of square roots, such as the square root of 87, is crucial in various mathematical and real-world applications. It is used in algebra to solve equations, in geometry to calculate distances and sizes of figures, and in many fields of science and engineering for a wide range of calculations. The ability to calculate square roots efficiently and accurately is, therefore, an essential skill.
What is the square root of 87?
+The square root of 87 is approximately 9.33. This is the number that, when multiplied by itself, gives 87.
How can I calculate the square root of 87?
+You can calculate the square root of 87 using a calculator, the long division method, or the Babylonian method. Each method has its own advantages and can provide the square root to varying degrees of precision.
Why is calculating the square root of 87 important?
+Calculating the square root of 87, or any number, is important because it has numerous applications in mathematics, science, engineering, and finance. Understanding square roots and how to calculate them is a fundamental skill that underlies many mathematical and real-world problems.
In conclusion, the calculation of the square root of 87 is a straightforward mathematical operation that can be performed using various methods, each with its own level of complexity and precision. Understanding how to calculate square roots and applying this knowledge in practical problems is essential for advancement in many fields. The square root of 87, approximately 9.33, is a specific example of how this mathematical operation can be applied to find the root of any given number.