The concept of square roots is a fundamental aspect of mathematics, particularly in algebra and geometry. At its core, the square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 16 is 4, because 4 multiplied by 4 equals 16. This operation is denoted by the symbol √, and it plays a crucial role in solving equations and understanding geometric shapes.
Understanding Square Roots

A deeper dive into square roots reveals that they can be categorized into two main types: real square roots and imaginary square roots. Real square roots are those that result in a real number, such as the square root of 1, which equals 1. On the other hand, imaginary square roots involve the square root of a negative number, which cannot be represented on the real number line and requires the use of complex numbers. The concept of square roots is essential in various mathematical disciplines, including calculus, where it is used to solve equations and understand the properties of functions.
Calculating Square Roots
Calculating square roots can be straightforward for perfect squares, but it becomes more complex for non-perfect squares. For example, the square root of 2 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on indefinitely without repeating. The calculation of square roots can be performed using various methods, including the long division method, the Babylonian method, or through the use of a calculator. Each method has its own set of advantages and is chosen based on the specific requirements of the problem at hand.
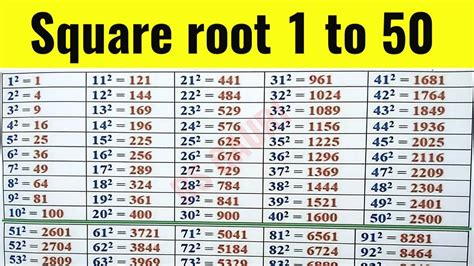
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
Key Points
- The square root of a number is a value that, when multiplied by itself, gives the original number.
- Real square roots result in real numbers, while imaginary square roots involve negative numbers and complex numbers.
- Calculating square roots can be done using various methods, including long division and the Babylonian method.
- The concept of square roots is fundamental in mathematics, with applications in algebra, geometry, calculus, and other disciplines.
- Understanding square roots is essential for solving equations, understanding geometric shapes, and grasping more advanced mathematical concepts.
In conclusion, the concept of square roots, particularly the square root of 1, serves as a foundational element in mathematics. Its simplicity belies its importance, as it underpins a wide range of mathematical operations and applications. Whether in the realm of real numbers or venturing into complex numbers, the square root operation remains a critical tool for mathematical exploration and problem-solving.
What is the square root of a negative number?
+The square root of a negative number is an imaginary number, which is a concept used in mathematics to extend the real number system to the complex number system. It is denoted by the symbol i, where i is the square root of -1.
How are square roots used in real-world applications?
+Square roots have numerous real-world applications, including physics, engineering, computer science, and finance. They are used in calculations involving distances, velocities, and accelerations, as well as in the design of electronic circuits, architectural structures, and financial models.
Can square roots be calculated without a calculator?
+Yes, square roots can be calculated without a calculator using various methods, such as the long division method, the Babylonian method, or through the use of square root tables. These methods may require more time and effort but provide a way to calculate square roots manually.



