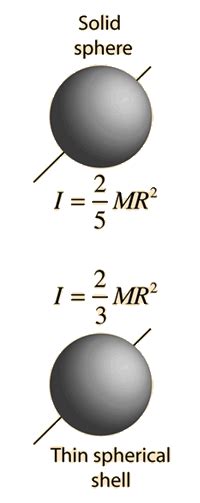The concept of rotational inertia, also known as moment of inertia, is a fundamental principle in physics that describes the tendency of an object to resist changes in its rotational motion. One of the most interesting and complex objects to study in this context is a sphere, due to its symmetrical shape and unique properties. In this article, we will delve into the world of sphere rotational inertia, exploring five key aspects that demonstrate the intricacies and applications of this phenomenon.
Understanding Rotational Inertia
Rotational inertia is a measure of an object’s resistance to changes in its rotational motion, and it depends on the object’s mass distribution and the axis of rotation. For a sphere, the rotational inertia is the same about any axis that passes through its center, due to its perfect symmetry. This property makes spheres particularly useful in various applications, from gyroscopes to roller bearings. The rotational inertia of a sphere can be calculated using the formula I = (2⁄5)mr^2, where I is the moment of inertia, m is the mass of the sphere, and r is its radius.
Calculating Rotational Inertia
To calculate the rotational inertia of a sphere, we need to know its mass and radius. For example, a bowling ball with a mass of 7.26 kg and a radius of 0.107 m has a rotational inertia of approximately 0.104 kg*m^2. This value represents the ball’s resistance to changes in its rotational motion, and it plays a crucial role in determining its overall motion and behavior. The calculation of rotational inertia is a critical step in understanding the dynamics of spherical objects and their applications in various fields.
| Object | Mass (kg) | Radius (m) | Rotational Inertia (kg*m^2) |
|---|---|---|---|
| Bowling Ball | 7.26 | 0.107 | 0.104 |
| Soccer Ball | 0.43 | 0.11 | 0.0063 |
| Planet Earth | 5.97 x 10^24 | 6.37 x 10^6 | 9.69 x 10^37 |
Applications of Sphere Rotational Inertia

The unique properties of sphere rotational inertia make it an essential concept in various fields, including engineering, physics, and astronomy. One of the most significant applications is in the design of gyroscopes, which rely on the conservation of angular momentum to maintain their orientation and stability. Spheres are also used in roller bearings, where their low friction and high rotational symmetry enable efficient and smooth motion. Additionally, the study of sphere rotational inertia has far-reaching implications for our understanding of planetary motion and the behavior of celestial bodies.
Planetary Motion and Celestial Mechanics
The rotational inertia of planets and other celestial bodies plays a crucial role in determining their motion and behavior. The conservation of angular momentum, which is closely related to rotational inertia, is a fundamental principle in celestial mechanics, governing the orbits of planets, moons, and asteroids. By studying the rotational inertia of these bodies, scientists can gain valuable insights into their composition, structure, and evolution. For example, the rotational inertia of the Earth is approximately 9.69 x 10^37 kg*m^2, which is a critical factor in determining its orbital period and axial precession.
Key Points
- The rotational inertia of a sphere is given by the formula I = (2/5)mr^2, where I is the moment of inertia, m is the mass of the sphere, and r is its radius.
- Spheres have unique properties that make them useful in various applications, including gyroscopes, roller bearings, and celestial mechanics.
- The calculation of rotational inertia is a critical step in understanding the dynamics of spherical objects and their applications in various fields.
- The study of sphere rotational inertia has significant implications for our understanding of planetary motion and the behavior of celestial bodies.
- The conservation of angular momentum, which is closely related to rotational inertia, is a fundamental principle in celestial mechanics, governing the orbits of planets, moons, and asteroids.
Conclusion and Future Directions
In conclusion, the concept of sphere rotational inertia is a complex and fascinating topic that has far-reaching implications for our understanding of the physical world. From the design of gyroscopes to the study of celestial mechanics, the unique properties of spheres make them an essential component of various systems and applications. As we continue to explore and understand the intricacies of sphere rotational inertia, we may uncover new and innovative ways to apply this knowledge in fields such as engineering, physics, and astronomy. By delving deeper into the world of rotational inertia, we can gain a deeper appreciation for the beauty and complexity of the physical world and uncover new secrets of the universe.
What is the formula for calculating the rotational inertia of a sphere?
+The formula for calculating the rotational inertia of a sphere is I = (2⁄5)mr^2, where I is the moment of inertia, m is the mass of the sphere, and r is its radius.
What are some common applications of sphere rotational inertia?
+Sphere rotational inertia has various applications, including gyroscopes, roller bearings, and celestial mechanics. It is also used in the design of spacecraft, industrial machinery, and other systems that require efficient and smooth motion.
How does the rotational inertia of a planet affect its motion and behavior?
+The rotational inertia of a planet plays a crucial role in determining its motion and behavior. It affects the planet’s orbital period, axial precession, and stability, and is closely related to the conservation of angular momentum, which is a fundamental principle in celestial mechanics.