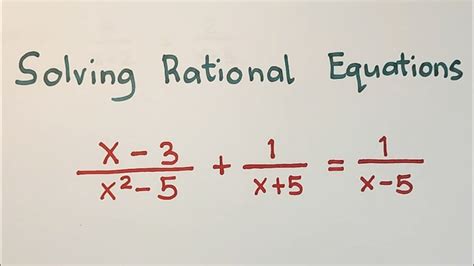Rational equations, which involve fractions with polynomials in both the numerator and denominator, can be intimidating to solve. However, with a systematic approach and understanding of the underlying principles, solving these equations can become straightforward. This article aims to guide you through the process of solving rational equations, highlighting key concepts, and providing illustrative examples to ensure a comprehensive understanding of the subject.
Key Points
- Understanding the structure of rational equations and their components
- Clearing fractions by multiplying by the least common denominator (LCD)
- Solving the resulting equation after clearing fractions
- Checking solutions for validity to avoid extraneous solutions
- Applying these principles to solve complex rational equations
Introduction to Rational Equations
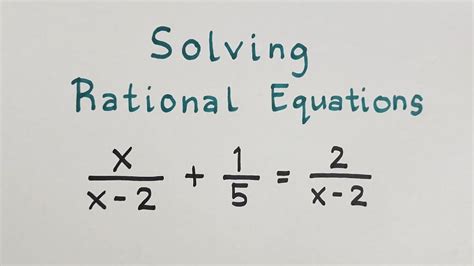
Rational equations are equations that contain one or more rational expressions, where a rational expression is a fraction of two polynomials. These equations can be simple, involving only linear expressions, or they can be complex, involving higher-degree polynomials. Solving rational equations involves isolating the variable, which can be complicated by the presence of fractions.
Understanding Rational Expressions
A rational expression is a quotient of two polynomials. For instance, \frac{2x+3}{x-4} is a rational expression. Understanding how to simplify, add, subtract, multiply, and divide rational expressions is crucial for solving rational equations. Simplifying rational expressions involves factoring the numerator and denominator and canceling out any common factors.
Solving Rational Equations

The primary step in solving rational equations is to eliminate the fractions. This is achieved by multiplying every term in the equation by the least common denominator (LCD) of all the fractions present in the equation. The LCD is the smallest expression that all denominators can divide into evenly.
Clearing Fractions
Consider the equation \frac{2}{x} + \frac{3}{x+1} = 1. To clear fractions, we first find the LCD, which in this case is x(x+1). Multiplying every term by x(x+1) gives us 2(x+1) + 3x = x(x+1). Simplifying both sides yields 2x + 2 + 3x = x^2 + x, which further simplifies to 5x + 2 = x^2 + x.
Solving the Resulting Equation
After clearing fractions, we solve the resulting equation. Continuing with our example, 5x + 2 = x^2 + x, we rearrange the terms to set the equation to zero: x^2 + x - 5x - 2 = 0, which simplifies to x^2 - 4x - 2 = 0. This quadratic equation can be solved by factoring, completing the square, or using the quadratic formula.
The quadratic formula is $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$, where $a$, $b$, and $c$ are coefficients from the quadratic equation $ax^2 + bx + c = 0$. Applying this to our equation, where $a = 1$, $b = -4$, and $c = -2$, we get $x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(-2)}}{2(1)}$.
Simplifying inside the square root gives $x = \frac{4 \pm \sqrt{16 + 8}}{2}$, which further simplifies to $x = \frac{4 \pm \sqrt{24}}{2}$. Simplifying $\sqrt{24}$ to $2\sqrt{6}$ gives $x = \frac{4 \pm 2\sqrt{6}}{2}$, and finally, $x = 2 \pm \sqrt{6}$.
Checking Solutions
After obtaining solutions, it’s crucial to check each solution in the original equation to ensure it’s not extraneous. Extraneous solutions can arise from the process of clearing fractions, as this process can introduce solutions that do not satisfy the original equation. Substituting x = 2 + \sqrt{6} and x = 2 - \sqrt{6} back into the original equation \frac{2}{x} + \frac{3}{x+1} = 1 will confirm whether these are valid solutions.
Importance of Checking Solutions
Checking solutions is a critical step that ensures the validity of the obtained solutions. This step is often overlooked but is essential in algebraic manipulations, especially when clearing fractions or squaring both sides of an equation, as these operations can introduce extraneous solutions.
| Step in Solving Rational Equations | Description |
|---|---|
| 1. Identify the LCD | Determine the least common denominator of all fractions in the equation. |
| 2. Clear Fractions | Multiply every term in the equation by the LCD to eliminate fractions. |
| 3. Simplify and Solve | Simplify the resulting equation and solve for the variable. |
| 4. Check Solutions | Substitute the solutions back into the original equation to verify their validity. |
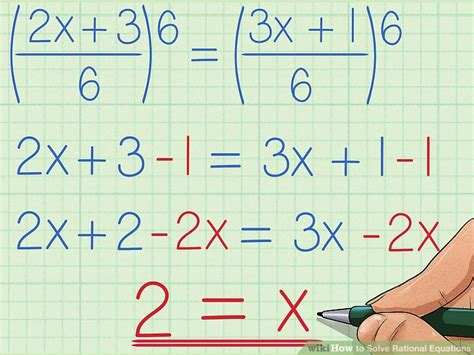
Advanced Techniques and Considerations
In addition to the basic steps outlined, solving rational equations may require advanced techniques, such as dealing with complex denominators, recognizing and factorizing quadratic expressions, and applying algebraic identities. Furthermore, understanding the concept of extraneous solutions and how they can arise from algebraic manipulations is crucial for accurately solving rational equations.
Complex Denominators and Quadratic Expressions
Situations may arise where the denominators are complex expressions or where the equation simplifies to a quadratic expression that does not factor easily. In such cases, using the quadratic formula or applying advanced factoring techniques may be necessary. Additionally, recognizing patterns that allow for simplification, such as difference of squares or sum/difference formulas, can be invaluable.
What is the first step in solving a rational equation?
+The first step is to identify and clear fractions by multiplying every term by the least common denominator (LCD) of all fractions in the equation.
Why is checking solutions important?
+Checking solutions is crucial to ensure that the solutions obtained are valid and not extraneous, which can be introduced during the process of clearing fractions or other algebraic manipulations.
What happens if the LCD is not correctly identified?
+If the LCD is not correctly identified, it may lead to incorrect clearing of fractions, resulting in an incorrect equation and potentially incorrect solutions.
In conclusion, solving rational equations requires a systematic approach, starting from understanding the structure of rational expressions, identifying the LCD, clearing fractions, solving the resulting equation, and finally, checking solutions to ensure their validity. By mastering these steps and understanding the underlying principles, individuals can confidently tackle rational equations, whether they are simple or complex.