The shell method formula, a fundamental concept in calculus, is used to calculate the volumes of solids of revolution. This technique is particularly useful when the axis of rotation is perpendicular to the axis of definition. The shell method, also known as the shell technique or shell integration, provides an alternative to the disk and washer methods for finding volumes of solids. Understanding the shell method formula is crucial for solving a wide range of problems in mathematics and physics, particularly in the fields of engineering and architecture.
Introduction to the Shell Method Formula
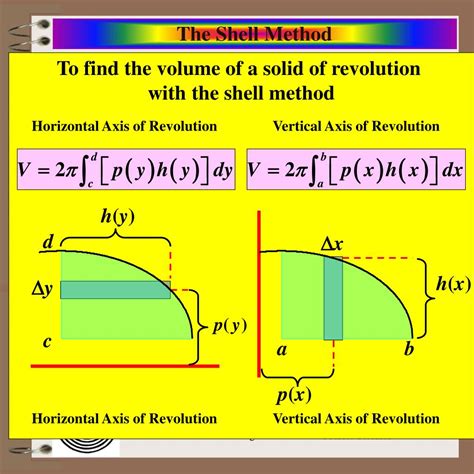
The shell method formula is derived from the idea of summing up the volumes of infinitesimally thin shells that make up the solid of revolution. The formula for the volume of a solid of revolution using the shell method is given by V = 2π∫[a,b] r(x)h(x) dx, where r(x) is the distance from the axis of rotation to the edge of the solid and h(x) is the height of the shell at x. This formula is the cornerstone of the shell method and is used to solve a variety of problems involving volumes of solids.
Key Points
- The shell method formula is used to calculate the volumes of solids of revolution.
- The formula is V = 2π∫[a,b] r(x)h(x) dx, where r(x) is the distance from the axis of rotation and h(x) is the height of the shell.
- The shell method is particularly useful when the axis of rotation is perpendicular to the axis of definition.
- This technique provides an alternative to the disk and washer methods for finding volumes of solids.
- Understanding the shell method formula is crucial for solving problems in mathematics, physics, engineering, and architecture.
Derivation of the Shell Method Formula
The derivation of the shell method formula begins with the concept of a solid of revolution. When a region bounded by a curve y = f(x), the x-axis, and the lines x = a and x = b is rotated about the y-axis, it generates a solid of revolution. The shell method involves dividing this solid into thin shells, each with a radius r(x) and a height h(x). The volume of each shell is approximately 2πr(x)h(x)dx, where dx is the thickness of the shell.
| Component | Description |
|---|---|
| r(x) | Distance from the axis of rotation to the edge of the solid |
| h(x) | Height of the shell at x |
| dx | Thickness of the shell |
| 2π | Constant factor representing the circumference of the shell |

Applying the Shell Method Formula

Applying the shell method formula involves several steps: identifying the region to be rotated, determining the axis of rotation, and setting up the integral for the volume. For example, if we want to find the volume of the solid generated by rotating the region bounded by y = x^2, y = 0, x = 0, and x = 2 about the y-axis, we would use the shell method formula with r(x) = x and h(x) = x^2.
The integral for the volume would be V = 2π∫[0,2] x(x^2) dx = 2π∫[0,2] x^3 dx. Evaluating this integral gives us the volume of the solid. This example illustrates the application of the shell method formula to a specific problem, demonstrating its utility in calculating volumes of solids of revolution.
Comparison with Other Methods
The shell method is one of several techniques used to find volumes of solids of revolution. The disk and washer methods are also commonly used, each with its own set of applications and advantages. The choice of method depends on the specific problem and the axis of rotation. Understanding the strengths and limitations of each method is essential for effectively solving volume problems.
In conclusion, the shell method formula provides a powerful tool for calculating the volumes of solids of revolution. Its application, however, requires a deep understanding of the underlying mathematics and the ability to identify the correct parameters for the formula. By mastering the shell method, individuals can solve a wide range of problems in mathematics and physics, contributing to advancements in fields such as engineering and architecture.
What is the shell method formula used for?
+The shell method formula is used to calculate the volumes of solids of revolution, particularly when the axis of rotation is perpendicular to the axis of definition.
How is the shell method formula derived?
+The shell method formula is derived by summing up the volumes of infinitesimally thin shells that make up the solid of revolution, with the volume of each shell approximated as 2πr(x)h(x)dx.
What are the key components of the shell method formula?
+The key components are r(x), the distance from the axis of rotation to the edge of the solid; h(x), the height of the shell at x; dx, the thickness of the shell; and 2π, a constant factor representing the circumference of the shell.
Meta Description: Learn how to apply the shell method formula to calculate volumes of solids of revolution. Understand the derivation, application, and comparison with other methods, and explore expert insights and FAQs for a comprehensive understanding.



