The SAT, a standardized test widely used for college admissions in the United States, is designed to assess a student's readiness for college. It focuses on testing the student's knowledge of reading, writing, and mathematics. To excel in the SAT, especially in the math section, having a comprehensive understanding of mathematical formulas and concepts is crucial. This guide aims to provide an overview of the key formulas and concepts that are commonly tested on the SAT, helping students prepare more effectively.
Key Points
- Understanding the format and content of the SAT math test is essential for effective preparation.
- Familiarity with algebra, geometry, trigonometry, and data analysis formulas is critical for solving SAT math problems.
- Practicing with sample questions and reviewing explanations can help in mastering these formulas and improving problem-solving skills.
- Developing a study plan that includes regular practice and review of mathematical concepts can significantly improve SAT scores.
- Utilizing online resources and study guides can provide additional support and practice opportunities for students preparing for the SAT.
Algebra Formulas
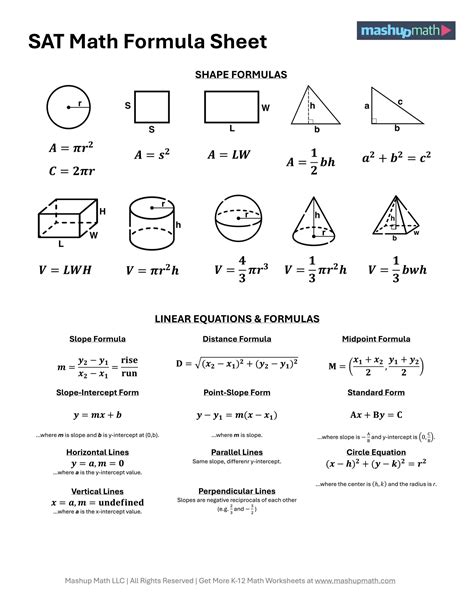
Algebra is a significant component of the SAT math section, covering topics such as linear equations, quadratic equations, functions, and systems of equations. Key formulas to remember include the slope-intercept form of a line (y = mx + b), where m is the slope and b is the y-intercept, and the quadratic formula, x = [-b ± sqrt(b^2 - 4ac)] / 2a, used to solve quadratic equations of the form ax^2 + bx + c = 0. Understanding how to apply these formulas in different contexts is vital for solving algebraic problems on the SAT.
Linear Equations and Functions
Linear equations, represented in the form of y = mx + b, are fundamental in algebra. The slope (m) and the y-intercept (b) are critical components that define the line’s orientation and position on the coordinate plane. Functions, which are relations between a set of inputs (called the domain) and a set of possible outputs (called the range), are also extensively tested. The concept of function notation, f(x), and understanding how to evaluate functions are essential skills for the SAT.
| Formula | Description |
|---|---|
| y = mx + b | Slope-intercept form of a line |
| x = [-b ± sqrt(b^2 - 4ac)] / 2a | Quadratic formula |
| f(x) = output | Function notation |
Geometry Formulas

Geometry is another critical area of the SAT math test, covering points, lines, angles, and planes, as well as properties of triangles, quadrilaterals, polygons, circles, and three-dimensional figures. Important formulas include the area and perimeter of basic shapes like triangles, rectangles, and circles. For instance, the area of a circle is given by A = πr^2, where r is the radius, and the circumference is C = 2πr. Understanding these geometric formulas and how to apply them to solve problems is essential for success on the SAT.
Properties of Triangles
Triangles are a fundamental geometric shape, and their properties are frequently tested on the SAT. This includes understanding types of triangles (equilateral, isosceles, scalene), triangle inequality, and properties like congruence and similarity. The Pythagorean theorem, a^2 + b^2 = c^2, where a and b are the lengths of the legs of a right triangle, and c is the length of the hypotenuse, is particularly important for solving problems involving right triangles.
Trigonometry Formulas
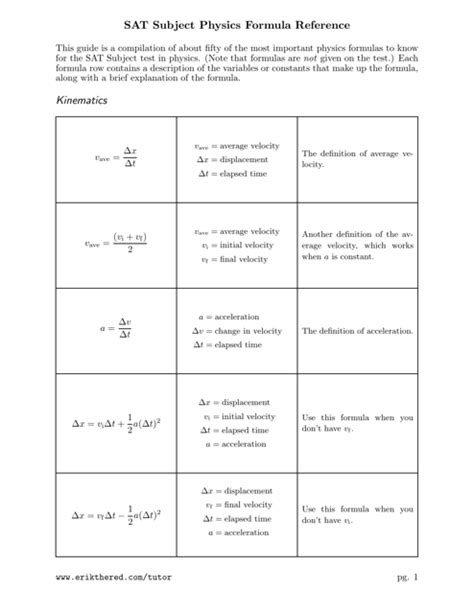
Trigonometry, the study of the relationships between the sides and angles of triangles, is also a component of the SAT math test. Key formulas include the definitions of sine, cosine, and tangent in a right triangle: sin(θ) = opposite side / hypotenuse, cos(θ) = adjacent side / hypotenuse, and tan(θ) = opposite side / adjacent side. Understanding these ratios and how to use them to solve problems involving right triangles is crucial for the SAT.
Identities and Equations
Trigonometric identities, such as the Pythagorean identity sin^2(θ) + cos^2(θ) = 1, and understanding how to solve basic trigonometric equations, are important concepts tested on the SAT. These skills are essential for solving problems that involve trigonometric functions and identities.
| Formula | Description |
|---|---|
| A = πr^2 | Area of a circle |
| C = 2πr | Circumference of a circle |
| a^2 + b^2 = c^2 | Pythagorean theorem |
| sin(θ) = opposite side / hypotenuse | Sine of an angle in a right triangle |
| cos(θ) = adjacent side / hypotenuse | Cosine of an angle in a right triangle |
| tan(θ) = opposite side / adjacent side | Tangent of an angle in a right triangle |
Data Analysis Formulas
Data analysis, including topics like charts, graphs, and statistical measures, is another area covered on the SAT. Understanding how to interpret data presented in tables, graphs, and charts, as well as calculating mean, median, mode, and range, is essential. The formula for the mean, (sum of all values) / (number of values), is particularly useful for solving data analysis problems.
Statistical Measures
Statistical measures such as mean, median, mode, and range are critical concepts in data analysis. The mean, or average, is calculated by summing all the values and dividing by the number of values. The median is the middle value in a list of numbers, the mode is the number that appears most frequently, and the range is the difference between the highest and lowest values. Understanding these measures and how to calculate them is vital for interpreting and analyzing data on the SAT.
What are the most important formulas to know for the SAT math section?
+The most important formulas include the slope-intercept form of a line, the quadratic formula, geometric formulas for area and perimeter, the Pythagorean theorem, trigonometric ratios, and statistical measures like mean, median, mode, and range.
How can I effectively study for the SAT math section?
+Effective studying for the SAT math section involves understanding the test format, practicing with sample questions, reviewing mathematical concepts, and developing a study plan that includes regular practice and review.
What resources are available to help me prepare for the SAT?
+Resources available for SAT preparation include official study guides, online practice tests, tutoring services, and mobile apps designed to help students review and practice mathematical concepts and problem-solving strategies.
In conclusion, mastering the formulas and concepts outlined in this guide is essential for achieving success on the SAT math section. By understanding the key formulas in algebra, geometry, trigonometry, and data analysis, and practicing how to apply them to solve problems, students can significantly improve their performance on the test. Remember, effective preparation involves a combination of understanding the test format, practicing with sample questions, reviewing mathematical concepts, and developing a study plan tailored to your needs.