The Routh-Hurwitz criterion is a fundamental concept in control systems engineering, used to determine the stability of a system. It provides a straightforward method to assess whether a system is stable, unstable, or marginally stable based on its characteristic equation. In this article, we will delve into the 5 ways the Routh-Hurwitz criterion is applied, exploring its theoretical foundations, practical applications, and the nuances of its implementation.
Key Points
- The Routh-Hurwitz criterion is used to determine the stability of a system based on its characteristic equation.
- It involves constructing a Routh array, which helps in identifying the number of roots of the characteristic equation that lie in the right half of the s-plane.
- The criterion is essential in control systems design, as it allows engineers to predict and ensure the stability of systems before they are implemented.
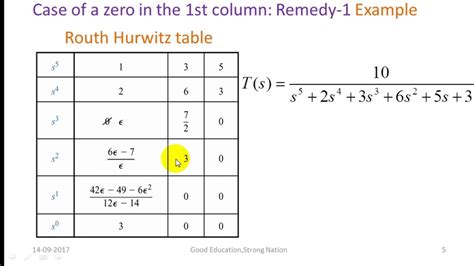
- There are limitations and special cases to consider when applying the Routh-Hurwitz criterion, including the presence of zeros in the first column of the Routh array.
- The criterion can be applied to both continuous and discrete-time systems, with appropriate modifications for the latter.
Understanding the Routh-Hurwitz Criterion

The Routh-Hurwitz criterion is named after Edward John Routh and Adolf Hurwitz, who independently developed this method in the late 19th century. It is based on the concept that a system is stable if all the roots of its characteristic equation have negative real parts. The characteristic equation of a system can be represented in the form of a_ns^n + a_{n-1}s^{n-1} + \cdots + a_1s + a_0 = 0, where s is the complex frequency variable and a_n, a_{n-1}, \ldots, a_1, a_0 are coefficients.
Constructing the Routh Array
To apply the Routh-Hurwitz criterion, one constructs a Routh array, which is a table of coefficients derived from the characteristic equation. The array is constructed by arranging the coefficients of the characteristic equation in rows, with each row representing the coefficients of the polynomial and its derivatives, evaluated at s = 0 and s = \infty. The first two rows of the array are filled with the coefficients of the characteristic equation, and subsequent rows are calculated using a specific formula that involves the coefficients from the two preceding rows.
| Row | Formula |
|---|---|
| 1st Row | $a_n, a_{n-2}, a_{n-4}, \ldots$ |
| 2nd Row | $a_{n-1}, a_{n-3}, a_{n-5}, \ldots$ |
| 3rd Row | Calculated using the formula involving the 1st and 2nd rows |
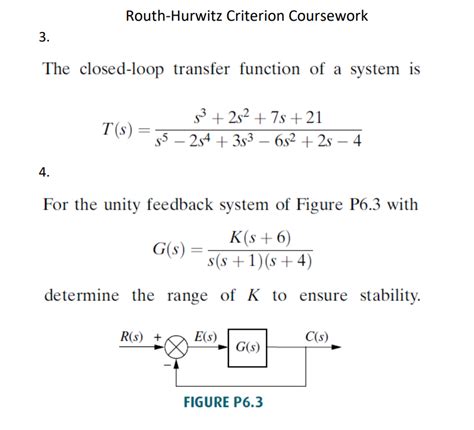
5 Ways the Routh-Hurwitz Criterion is Applied

The Routh-Hurwitz criterion is applied in various ways across different fields of engineering, including control systems, electrical engineering, and mechanical engineering. Here are five key applications:
1. Stability Analysis of Control Systems
The most direct application of the Routh-Hurwitz criterion is in the stability analysis of control systems. By examining the roots of the characteristic equation, engineers can determine whether a system is stable (all roots have negative real parts), unstable (at least one root has a positive real part), or marginally stable (at least one root has a zero real part).
2. Design of Control Systems
Knowing the stability of a system allows engineers to design control systems that meet specific stability requirements. This involves adjusting the parameters of the system (such as gains and time constants) to ensure that the system behaves as desired under various operating conditions.
3. Analysis of Electrical Circuits
In electrical engineering, the Routh-Hurwitz criterion is used to analyze the stability of electrical circuits. This is particularly important in the design of filters, amplifiers, and other electronic circuits, where stability is crucial for proper operation.
4. Mechanical System Stability
The criterion is also applied in mechanical engineering to assess the stability of mechanical systems, such as vibration systems and robotic arms. By analyzing the roots of the characteristic equation, engineers can predict the behavior of these systems under different conditions.
5. Discrete-Time Systems Analysis
While the Routh-Hurwitz criterion is primarily used for continuous-time systems, it can be adapted for discrete-time systems by transforming the discrete-time characteristic equation into a form that is amenable to Routh-Hurwitz analysis. This involves using the z-transform instead of the Laplace transform.
Conclusion and Future Directions
In conclusion, the Routh-Hurwitz criterion is a versatile and essential tool in the field of control systems engineering, with applications extending into various domains of engineering. Its ability to predict system stability based on the characteristic equation makes it an indispensable method for ensuring the stability and performance of systems. As engineering fields continue to evolve, the importance of stability analysis will only grow, making the Routh-Hurwitz criterion a timeless and valuable contribution to the discipline.
What is the primary use of the Routh-Hurwitz criterion in control systems engineering?
+The primary use of the Routh-Hurwitz criterion is to determine the stability of a system based on its characteristic equation, allowing engineers to predict whether a system is stable, unstable, or marginally stable.
How is the Routh array constructed for a given characteristic equation?
+The Routh array is constructed by arranging the coefficients of the characteristic equation in rows, with each row representing the coefficients of the polynomial and its derivatives, evaluated at s = 0 and s = \infty. Subsequent rows are calculated using a specific formula involving the coefficients from the two preceding rows.
Can the Routh-Hurwitz criterion be applied to discrete-time systems?
+Yes, the Routh-Hurwitz criterion can be adapted for discrete-time systems by transforming the discrete-time characteristic equation into a form that is amenable to Routh-Hurwitz analysis, typically involving the use of the z-transform instead of the Laplace transform.