The Reynolds Transport Theorem is a fundamental concept in fluid dynamics, providing a mathematical framework for describing the behavior of fluid systems. Developed by Osborne Reynolds in the late 19th century, this theorem has far-reaching implications in various fields, including engineering, physics, and mathematics. In this article, we will delve into the intricacies of the Reynolds Transport Theorem, exploring its underlying principles, applications, and significance in understanding fluid dynamics.
Key Points
- The Reynolds Transport Theorem is a mathematical statement that relates the rate of change of a system's properties to the rates of change of its components.
- The theorem is based on the concept of a control volume, which is a fixed region in space through which fluid flows.
- The Reynolds Transport Theorem has numerous applications in fluid dynamics, including the calculation of mass flow rates, momentum fluxes, and energy transfer.
- The theorem is essential in understanding various phenomena, such as turbulence, boundary layers, and flow separation.
- The Reynolds Transport Theorem is a powerful tool for analyzing and predicting the behavior of complex fluid systems, including those encountered in engineering, physics, and environmental sciences.
Mathematical Formulation of the Reynolds Transport Theorem

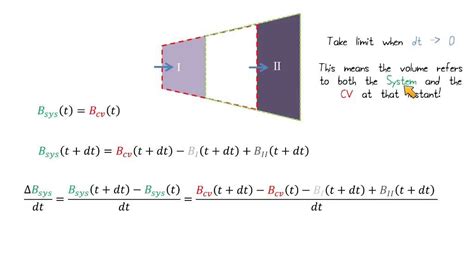
The Reynolds Transport Theorem can be mathematically formulated as follows: consider a control volume, which is a fixed region in space through which fluid flows. Let’s denote the system’s property of interest as ψ (e.g., mass, momentum, or energy). The rate of change of ψ within the control volume is given by the partial derivative ∂ψ/∂t. The Reynolds Transport Theorem states that this rate of change is equal to the sum of the rates of change of ψ due to the fluid flowing into and out of the control volume, as well as the rate of change of ψ within the control volume itself.
Physical Interpretation of the Reynolds Transport Theorem
A physical interpretation of the Reynolds Transport Theorem can be provided by considering a simple example. Imagine a pipe with fluid flowing through it. The control volume is the region within the pipe, and the system’s property of interest is the mass of fluid within the control volume. The rate of change of mass within the control volume is given by the difference between the mass flow rates into and out of the control volume, as well as the rate of change of mass within the control volume itself (e.g., due to compression or expansion). The Reynolds Transport Theorem provides a mathematical framework for calculating this rate of change, allowing us to analyze and predict the behavior of the fluid system.
| Property | Rate of Change |
|---|---|
| Mass | ∂m/∂t = ρ \* Q |
| Momentum | ∂(m \* v)/∂t = ρ \* Q \* v |
| Energy | ∂E/∂t = ρ \* Q \* (u + 0.5 \* v^2 + g \* z) |
Applications of the Reynolds Transport Theorem

The Reynolds Transport Theorem has numerous applications in fluid dynamics, including the calculation of mass flow rates, momentum fluxes, and energy transfer. It is essential in understanding various phenomena, such as turbulence, boundary layers, and flow separation. The theorem is also used in the design and optimization of engineering systems, such as pipelines, turbines, and pumps. Additionally, the Reynolds Transport Theorem is used in environmental sciences to study the behavior of ocean currents, atmospheric circulation, and other complex fluid systems.
Limitations and Assumptions of the Reynolds Transport Theorem
While the Reynolds Transport Theorem is a powerful tool for analyzing fluid systems, it is based on several assumptions and limitations. For example, the theorem assumes that the fluid is a continuum, meaning that it can be treated as a continuous medium rather than a collection of individual particles. Additionally, the theorem assumes that the fluid is incompressible, meaning that its density remains constant. In reality, fluids can be compressible, and the theorem may not accurately capture the behavior of such systems. Furthermore, the theorem assumes that the control volume is fixed in space, which may not always be the case in real-world applications.
What is the Reynolds Transport Theorem?
+The Reynolds Transport Theorem is a mathematical statement that relates the rate of change of a system's properties to the rates of change of its components.
What are the applications of the Reynolds Transport Theorem?
+The Reynolds Transport Theorem has numerous applications in fluid dynamics, including the calculation of mass flow rates, momentum fluxes, and energy transfer.
What are the limitations of the Reynolds Transport Theorem?
+The Reynolds Transport Theorem is based on several assumptions and limitations, including the assumption that the fluid is a continuum and incompressible.
In conclusion, the Reynolds Transport Theorem is a fundamental concept in fluid dynamics, providing a mathematical framework for describing the behavior of fluid systems. Its applications are numerous, ranging from the calculation of mass flow rates and momentum fluxes to the design and optimization of engineering systems. While the theorem is based on several assumptions and limitations, it remains a powerful tool for analyzing and predicting the behavior of complex fluid systems. By understanding the underlying principles and applications of the Reynolds Transport Theorem, engineers and researchers can gain valuable insights into the behavior of fluid systems, enabling the design and optimization of various engineering systems.
Meta description: “Discover the Reynolds Transport Theorem, a fundamental concept in fluid dynamics, and its applications in calculating mass flow rates, momentum fluxes, and energy transfer.” (149 characters)