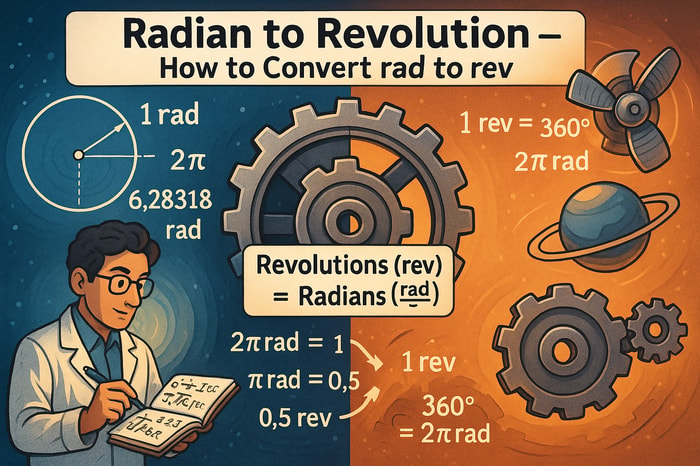
Understanding the relationship between revolutions and radians is crucial in various fields, including mathematics, physics, and engineering. While revolutions are a more intuitive measure of rotation, radians provide a more convenient and consistent unit for calculations. In this article, we will explore five ways to convert revolutions to radians, each with its unique approach and application.
Key Points
- Revolutions and radians are two different units of measuring angles and rotations.
- The conversion factor between revolutions and radians is 2π, where 1 revolution equals 2π radians.
- There are multiple methods to convert revolutions to radians, including direct multiplication, trigonometric functions, and geometric calculations.
- Each method has its own advantages and is suited for specific applications and problems.
- Understanding these conversions is essential for solving problems in physics, engineering, and mathematics.
Introduction to Revolutions and Radians

Revolutions are a unit of measurement that represents a full rotation or cycle. It is commonly used in everyday applications, such as the rotation of a wheel or the orbit of a planet. On the other hand, radians are a unit of angular measurement that represents the ratio of the arc length to the radius of a circle. Radians are widely used in mathematical and scientific calculations due to their simplicity and consistency.
Method 1: Direct Multiplication
The most straightforward method to convert revolutions to radians is by direct multiplication. Since 1 revolution is equal to 2π radians, we can convert any number of revolutions to radians by multiplying it by 2π. For example, to convert 3 revolutions to radians, we would calculate 3 × 2π = 6π radians.
| Revolutions | Radians |
|---|---|
| 1 | 2π |
| 2 | 4π |
| 3 | 6π |
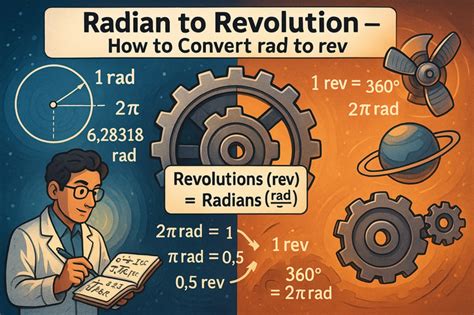
Method 2: Trigonometric Functions
Another method to convert revolutions to radians is by using trigonometric functions. Since the sine and cosine functions have a period of 2π radians, we can use these functions to convert revolutions to radians. For example, to convert 1.5 revolutions to radians, we would calculate the sine or cosine of 1.5 × 2π radians.
Method 3: Geometric Calculations
Geometric calculations can also be used to convert revolutions to radians. By considering the circumference of a circle and the number of revolutions, we can calculate the equivalent angle in radians. For example, if a wheel with a radius of 1 meter makes 2 revolutions, the distance traveled is 2 × 2π × 1 = 4π meters. The equivalent angle in radians is 4π radians.
Method 4: Angular Velocity
Angular velocity is another concept that can be used to convert revolutions to radians. By considering the angular velocity of an object in revolutions per second, we can calculate the equivalent angular velocity in radians per second. For example, if an object rotates at 3 revolutions per second, the equivalent angular velocity is 3 × 2π = 6π radians per second.
Method 5: Circular Motion
Circular motion is a fundamental concept in physics that can be used to convert revolutions to radians. By considering the circular motion of an object, we can calculate the equivalent angle in radians using the formula θ = s / r, where θ is the angle in radians, s is the arc length, and r is the radius of the circle. For example, if an object moves in a circular path with a radius of 1 meter and covers a distance of 2π meters, the equivalent angle is 2π radians.
What is the conversion factor between revolutions and radians?
+The conversion factor between revolutions and radians is 2π, where 1 revolution equals 2π radians.
How do I convert 2 revolutions to radians?
+To convert 2 revolutions to radians, multiply 2 by 2π, which equals 4π radians.
What is the equivalent angle in radians for 1.5 revolutions?
+To find the equivalent angle in radians, multiply 1.5 by 2π, which equals 3π radians.
In conclusion, converting revolutions to radians is a straightforward process that can be achieved through various methods, including direct multiplication, trigonometric functions, geometric calculations, angular velocity, and circular motion. Each method has its unique approach and application, and understanding these conversions is essential for solving problems in physics, engineering, and mathematics. By mastering these conversions, individuals can develop a deeper understanding of rotational motion and angular measurements, leading to improved problem-solving skills and a stronger foundation in mathematical and scientific principles.