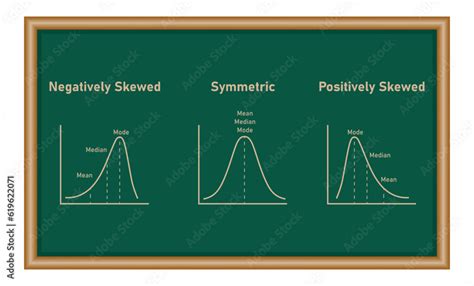
The concept of skewness is a fundamental aspect of statistical analysis, providing valuable insights into the distribution of data. In essence, skewness refers to the asymmetry or lack of symmetry in a probability distribution. There are several types of skewness, each with distinct characteristics and implications for data interpretation. Understanding these types is crucial for accurate analysis and informed decision-making. In this article, we will delve into the five primary skewness types, exploring their definitions, examples, and practical applications.
Key Points
- Skewness is a measure of the asymmetry of a probability distribution.
- There are five primary types of skewness: positive, negative, zero, mesokurtic, and leptokurtic.
- Each type of skewness has distinct implications for data analysis and interpretation.
- Understanding skewness is crucial for selecting appropriate statistical methods and models.
- Skewness can be influenced by outliers, sample size, and data transformation.
Understanding Skewness Types
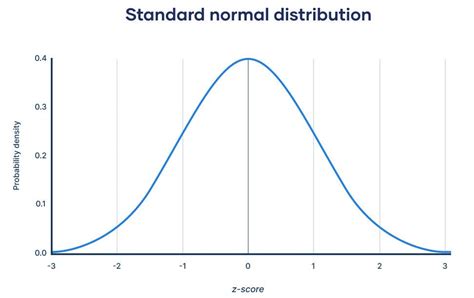
Skewness can be categorized into five main types, each representing a different degree of asymmetry. These types are not mutually exclusive, and a distribution can exhibit characteristics of multiple types. The five skewness types are: positive skewness, negative skewness, zero skewness, mesokurtic skewness, and leptokurtic skewness.
Positive Skewness
A distribution is said to be positively skewed if it has a longer tail on the right side. This means that the majority of the data points are concentrated on the left side of the distribution, with a few extreme values on the right side. Positive skewness is often observed in distributions of income, stock prices, and other economic variables. For example, the distribution of household incomes in a country may be positively skewed, with most households having lower incomes and a few households having very high incomes.
Negative Skewness
A distribution is said to be negatively skewed if it has a longer tail on the left side. This means that the majority of the data points are concentrated on the right side of the distribution, with a few extreme values on the left side. Negative skewness is often observed in distributions of exam scores, where most students score high grades and a few students score very low grades. For instance, the distribution of scores on a math test may be negatively skewed, with most students scoring above average and a few students scoring below average.
Zero Skewness
A distribution is said to be symmetric or have zero skewness if it is perfectly symmetric around the mean. This means that the distribution has equal proportions of data points on both sides of the mean. Zero skewness is often observed in distributions of random variables, such as the standard normal distribution. For example, the distribution of heights of adults in a population may be symmetric, with equal proportions of people taller and shorter than the mean height.
Mesokurtic Skewness
A distribution is said to be mesokurtic if it has a similar shape to the normal distribution. This means that the distribution has a moderate level of skewness, with a slight asymmetry around the mean. Mesokurtic skewness is often observed in distributions of financial variables, such as stock returns and interest rates. For instance, the distribution of daily stock returns may be mesokurtic, with a moderate level of skewness and a slight asymmetry around the mean return.
Leptokurtic Skewness
A distribution is said to be leptokurtic if it has a more extreme shape than the normal distribution. This means that the distribution has a high level of skewness, with a long tail and a high peak. Leptokurtic skewness is often observed in distributions of extreme events, such as natural disasters and financial crises. For example, the distribution of earthquake magnitudes may be leptokurtic, with a high level of skewness and a long tail of extreme events.
| SKEWNESS TYPE | DESCRIPTION | EXAMPLE |
|---|---|---|
| Positive Skewness | Longer tail on the right side | Household incomes |
| Negative Skewness | Longer tail on the left side | Exam scores |
| Zero Skewness | Perfectly symmetric around the mean | Heights of adults |
| Mesokurtic Skewness | Similar shape to the normal distribution | Stock returns |
| Leptokurtic Skewness | More extreme shape than the normal distribution | Earthquake magnitudes |

Practical Applications of Skewness
Skewness has numerous practical applications in various fields, including finance, economics, and engineering. For instance, skewness can be used to evaluate the risk of investment portfolios, predict the likelihood of extreme events, and optimize system performance. By understanding the skewness type, decision-makers can make informed choices and develop effective strategies to mitigate risks and capitalize on opportunities.
Skewness in Finance
In finance, skewness is used to evaluate the risk of investment portfolios and predict the likelihood of extreme events, such as stock market crashes. For example, a portfolio with a positively skewed distribution of returns may be more attractive to investors who are willing to take on higher risks in pursuit of higher returns. On the other hand, a portfolio with a negatively skewed distribution of returns may be more appealing to risk-averse investors who prioritize capital preservation.
Skewness in Economics
In economics, skewness is used to analyze the distribution of income and wealth. For instance, a country with a positively skewed distribution of income may have a larger proportion of low-income households, while a country with a negatively skewed distribution of income may have a larger proportion of high-income households. By understanding the skewness type, policymakers can develop targeted interventions to address income inequality and promote economic growth.
What is the difference between positive and negative skewness?
+Positive skewness refers to a distribution with a longer tail on the right side, while negative skewness refers to a distribution with a longer tail on the left side.
How does skewness affect data analysis?
+Skewness can affect the choice of statistical methods and models, as well as the interpretation of results. Understanding the skewness type is crucial for accurate data analysis and interpretation.
What are some common examples of skewness in real-world data?
+Common examples of skewness include household incomes, exam scores, stock returns, and earthquake magnitudes. Each of these examples exhibits a unique skewness type, which can be used to inform decision-making and strategy development.
In conclusion, understanding the different types of skewness is essential for accurate data analysis and interpretation. By recognizing the skewness type, researchers and analysts can select the most appropriate statistical methods and models, ensuring that their conclusions are reliable and valid. Moreover, skewness has numerous practical applications in various fields, including finance, economics, and engineering. As such, it is crucial to incorporate skewness into decision-making processes, developing effective strategies to mitigate risks and capitalize on opportunities.