The P-hat symbol, denoted as $\hat{p}$, is a statistical notation used to represent the sample proportion. It is a crucial concept in statistics, particularly in hypothesis testing and confidence intervals. In this article, we will explore five ways the P-hat symbol is used in statistical analysis, highlighting its significance and application in various contexts.
Introduction to P-hat Symbol
The P-hat symbol is used to estimate the population proportion based on a sample of data. It is calculated as the number of successes (or occurrences of a specific event) divided by the total number of trials (or sample size). The formula for calculating the P-hat symbol is \hat{p} = \frac{x}{n}, where x is the number of successes and n is the sample size.
Key Points
- The P-hat symbol is used to estimate the population proportion.
- It is calculated as the number of successes divided by the sample size.
- The P-hat symbol is used in hypothesis testing and confidence intervals.
- It is essential in statistical analysis to make inferences about a population.
- The P-hat symbol has various applications in fields such as medicine, social sciences, and business.
1. Hypothesis Testing
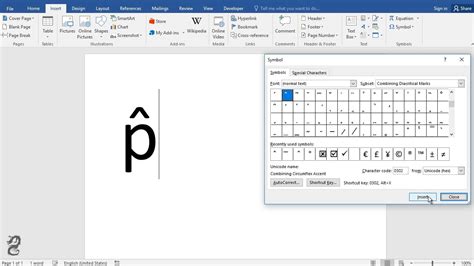
In hypothesis testing, the P-hat symbol is used to test a null hypothesis about a population proportion. For example, a researcher may want to test the hypothesis that the proportion of people who prefer a particular brand of coffee is 0.5. The P-hat symbol is used to calculate the test statistic, which is then compared to a critical value or a p-value to determine whether the null hypothesis should be rejected.
Example of Hypothesis Testing
Suppose a researcher wants to test the hypothesis that the proportion of people who prefer a particular brand of coffee is 0.5. A sample of 100 people is taken, and 60 people prefer the brand. The P-hat symbol is calculated as \hat{p} = \frac{60}{100} = 0.6. The test statistic is then calculated using the formula z = \frac{\hat{p} - p}{\sqrt{\frac{p(1-p)}{n}}}. If the p-value is less than the significance level, the null hypothesis is rejected, indicating that the proportion of people who prefer the brand is not 0.5.
| Sample Size | Number of Successes | P-hat Symbol |
|---|---|---|
| 100 | 60 | 0.6 |
| 200 | 120 | 0.6 |
| 500 | 300 | 0.6 |

2. Confidence Intervals
Confidence intervals are used to estimate a population parameter, such as the population proportion. The P-hat symbol is used to calculate the confidence interval, which provides a range of values within which the population proportion is likely to lie. The formula for calculating the confidence interval is \hat{p} \pm z \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}.
Example of Confidence Interval
Suppose a researcher wants to estimate the proportion of people who prefer a particular brand of coffee. A sample of 100 people is taken, and 60 people prefer the brand. The P-hat symbol is calculated as \hat{p} = \frac{60}{100} = 0.6. The confidence interval is then calculated using the formula \hat{p} \pm z \times \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}. If the confidence interval does not contain the value 0.5, it can be concluded that the proportion of people who prefer the brand is not 0.5.
3. Statistical Process Control
Statistical process control is used to monitor and control a process, such as a manufacturing process. The P-hat symbol is used to calculate the proportion of defective products, which is then used to determine whether the process is in control or not.
Example of Statistical Process Control
Suppose a manufacturer wants to monitor the proportion of defective products. A sample of 100 products is taken, and 10 products are found to be defective. The P-hat symbol is calculated as \hat{p} = \frac{10}{100} = 0.1. If the P-hat symbol is greater than the upper control limit, it indicates that the process is out of control, and corrective action is needed.
4. Quality Control

Quality control is used to ensure that a product meets certain standards. The P-hat symbol is used to calculate the proportion of products that meet the standards, which is then used to determine whether the product is of acceptable quality or not.
Example of Quality Control
Suppose a manufacturer wants to ensure that a product meets certain standards. A sample of 100 products is taken, and 90 products meet the standards. The P-hat symbol is calculated as \hat{p} = \frac{90}{100} = 0.9. If the P-hat symbol is greater than the acceptable quality level, it indicates that the product is of acceptable quality.
5. Medical Research
The P-hat symbol is used in medical research to estimate the proportion of people who respond to a treatment. For example, a researcher may want to estimate the proportion of people who respond to a new medication. The P-hat symbol is used to calculate the confidence interval, which provides a range of values within which the population proportion is likely to lie.
What is the P-hat symbol?
+The P-hat symbol is a statistical notation used to represent the sample proportion.
How is the P-hat symbol calculated?
+The P-hat symbol is calculated as the number of successes divided by the sample size.
What is the significance of the P-hat symbol in hypothesis testing?
+The P-hat symbol is used to test a null hypothesis about a population proportion.
What is the application of the P-hat symbol in quality control?
+The P-hat symbol is used to calculate the proportion of products that meet certain standards.
What is the importance of the P-hat symbol in medical research?
+The P-hat symbol is used to estimate the proportion of people who respond to a treatment.
In conclusion, the P-hat symbol is a crucial concept in statistical analysis, with various applications in fields such as hypothesis testing, confidence intervals, statistical process control, quality control, and medical research. Its significance lies in its ability to estimate a population proportion based on a sample of data, allowing researchers to make inferences about a population. By understanding the P-hat symbol and its applications, researchers can make informed decisions and draw meaningful conclusions from their data.
Meta Description: The P-hat symbol is a statistical notation used to represent the sample proportion, with applications in hypothesis testing, confidence intervals, and more. Learn about its significance and uses in this article. (145 characters)