Understanding numbers in expanded form is a fundamental concept in mathematics, particularly in the realm of basic arithmetic operations and number theory. Expanded form, also known as expanded notation, is a way of expressing numbers by breaking them down into their place values. This method is essential for comprehending how numbers are constructed and for performing arithmetic operations such as addition, subtraction, multiplication, and division. In this article, we will delve into the concept of numbers in expanded form, exploring what it entails, its significance, and how it is applied in mathematical operations.
Key Points
- Definition and explanation of expanded form
- Importance of expanded form in mathematical operations
- Examples of converting numbers to expanded form
- Application of expanded form in real-world scenarios
- Step-by-step guide on performing arithmetic operations using expanded form
Understanding Expanded Form
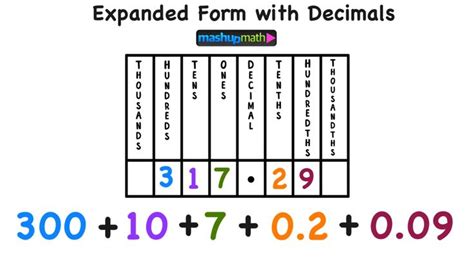
Expanded form is a method of representing a number by showing the value of each digit based on its position. For instance, the number 456 in expanded form is written as 400 + 50 + 6. Here, the digit 4 is in the hundreds place, 5 is in the tens place, and 6 is in the ones place. This representation helps in understanding the actual value of each digit within a number and facilitates the performance of arithmetic operations.
Significance of Expanded Form
The significance of expanded form lies in its ability to simplify complex arithmetic operations. By breaking down numbers into their place values, it becomes easier to add, subtract, multiply, or divide them. Expanded form also plays a crucial role in understanding the concept of regrouping in arithmetic operations, which is essential for accuracy in calculations. Furthermore, it aids in developing problem-solving skills and enhances the understanding of mathematical concepts.
| Number | Expanded Form |
|---|---|
| 123 | 100 + 20 + 3 |
| 456 | 400 + 50 + 6 |
| 789 | 700 + 80 + 9 |
Performing Arithmetic Operations Using Expanded Form

Expanded form makes arithmetic operations more intuitive and systematic. For example, when adding two numbers, we can align their expanded forms and add the corresponding place values. This method reduces the likelihood of errors and enhances computational efficiency. Similarly, subtraction, multiplication, and division can be performed by manipulating the expanded forms of the numbers involved.
Real-World Applications of Expanded Form
Beyond the realm of mathematics, expanded form has practical applications in various fields. In finance, understanding the expanded form of numbers is essential for managing budgets, calculating interest rates, and performing other financial calculations. In science, expanded form is used in measurements and data analysis. The concept is also integral to computer programming, where numbers are represented in binary form, a base-2 number system that relies on the principles of expanded notation.
What is the primary purpose of representing numbers in expanded form?
+The primary purpose is to understand the value of each digit within a number based on its position, facilitating easier arithmetic operations and a deeper understanding of mathematical concepts.
How does expanded form aid in performing arithmetic operations?
+It simplifies operations by allowing the alignment and addition/subtraction of corresponding place values, reducing errors and enhancing computational efficiency.
What are some real-world applications of expanded form?
+Expanded form has applications in finance for budget management and interest calculations, in science for measurements and data analysis, and in computer programming for representing binary numbers.
In conclusion, the concept of numbers in expanded form is a foundational element of mathematics, offering a deeper understanding of number structure and facilitating the performance of arithmetic operations. Its significance extends beyond mathematical operations, with practical applications in various fields that rely on numerical computations and data analysis. By grasping the concept of expanded form, individuals can enhance their mathematical skills, develop problem-solving abilities, and appreciate the intricacies of numerical representations.