The concept of a number line with negatives is a fundamental idea in mathematics, particularly in the realm of algebra and arithmetic. A number line is a visual representation of numbers on a line, where each point on the line corresponds to a specific number. The number line stretches infinitely in both directions, with positive numbers to the right of zero and negative numbers to the left. In this explanation, we will delve into the world of number lines with negatives, exploring their properties, applications, and importance in mathematical problem-solving.
Understanding the Basics of Number Lines
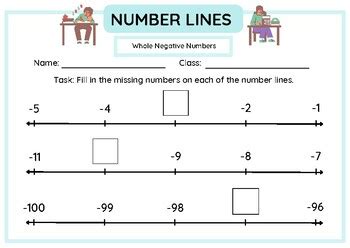
A standard number line consists of a horizontal line with numbers marked at regular intervals. The point labeled “0” is the origin, which separates the positive and negative number regions. Positive numbers are represented to the right of the origin, while negative numbers are represented to the left. The distance between each number on the line is equal, and the line extends infinitely in both directions. This visual representation helps students and mathematicians alike to better comprehend the relationships between numbers and perform arithmetic operations.
Introduction to Negative Numbers
Negative numbers are a crucial aspect of the number line, and they can be a bit tricky to grasp at first. Negative numbers represent quantities that are less than zero. For example, -3 is a negative number that is three units less than zero. When working with negative numbers on the number line, it’s essential to remember that moving to the left of zero means decreasing the value, while moving to the right means increasing the value. This concept is vital in various mathematical contexts, such as solving linear equations and graphing functions.
| Number Line Region | Description |
|---|---|
| Positive Numbers | Numbers greater than zero, represented to the right of the origin |
| Negative Numbers | Numbers less than zero, represented to the left of the origin |
| Origin (0) | The point that separates positive and negative numbers |

Key Properties of Number Lines with Negatives
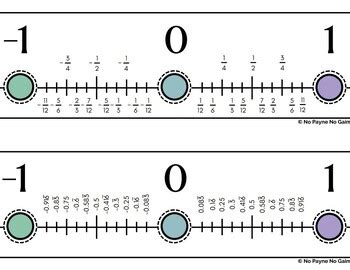
Number lines with negatives have several key properties that are essential to understand:
- Symmetry: The number line is symmetric around the origin, meaning that for every positive number, there is a corresponding negative number with the same absolute value.
- Distance: The distance between each number on the line is equal, allowing for accurate measurements and calculations.
- Direction: Moving to the right of the origin increases the value, while moving to the left decreases the value.
- Infinity: The number line extends infinitely in both directions, representing an endless range of positive and negative numbers.
Applications of Number Lines with Negatives
Number lines with negatives have numerous applications in mathematics, science, and real-world problem-solving. Some examples include:
- Linear Equations: Number lines are used to graph linear equations and solve problems involving slope and intercept.
- Graphing Functions: Number lines are essential in graphing functions, such as quadratic and polynomial equations.
- Financial Transactions: Negative numbers are used to represent debts or overdrafts in financial transactions.
- Temperature Scales: Negative numbers are used to represent temperatures below zero on temperature scales, such as Celsius and Fahrenheit.
Key Points
- Number lines with negatives are a fundamental concept in mathematics, representing a visual relationship between numbers.
- Negative numbers represent quantities less than zero and are essential in various mathematical contexts.
- The number line is symmetric around the origin, with equal distances between each number.
- Number lines with negatives have numerous applications in mathematics, science, and real-world problem-solving.
- Understanding number lines with negatives is crucial for solving linear equations, graphing functions, and working with financial transactions.
In conclusion, number lines with negatives are a powerful tool for understanding mathematical relationships and performing arithmetic operations. By grasping the concept of negative numbers and the properties of number lines, individuals can develop a deeper understanding of mathematics and improve their problem-solving skills. Whether in academic or real-world contexts, number lines with negatives play a vital role in representing and analyzing quantitative information.
What is the purpose of a number line with negatives?
+The purpose of a number line with negatives is to provide a visual representation of the relationship between numbers, including negative numbers, and to facilitate arithmetic operations and problem-solving.
How do negative numbers work on a number line?
+Negative numbers on a number line represent quantities less than zero. Moving to the left of zero decreases the value, while moving to the right increases the value.
What are some real-world applications of number lines with negatives?
+Number lines with negatives have numerous applications in finance, science, and everyday problem-solving, such as representing debts, temperatures below zero, and graphing functions.