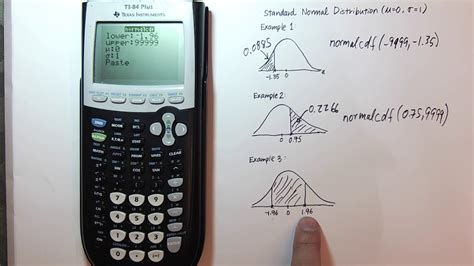
When it comes to working with statistical models, particularly the normal model, having the right tools and understanding the intricacies of these tools is crucial. A normal model calculator, designed to handle calculations related to the normal distribution, is an indispensable asset for statisticians and data analysts. The normal distribution, also known as the Gaussian distribution, is a probability distribution that is symmetric about the mean, indicating that data near the mean are more frequent in occurrence than data far from the mean. In this context, leveraging a normal model calculator effectively can significantly streamline the analysis process, ensuring accuracy and efficiency. Here are five tips for using a normal model calculator to its fullest potential:
Understanding the Normal Distribution Basics
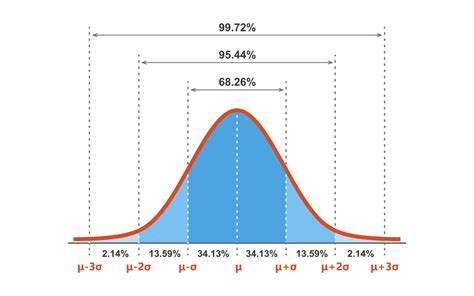
Before diving into the calculator tips, it’s essential to have a solid grasp of the normal distribution basics. The normal distribution is characterized by its mean (μ) and standard deviation (σ), parameters that define the shape and spread of the distribution. The mean indicates the central tendency of the data, while the standard deviation measures the variability or dispersion from the mean. Understanding these concepts is vital for interpreting the results from a normal model calculator.
Tip 1: Identifying the Parameters
The first step in using a normal model calculator is identifying the parameters of the distribution you’re working with. This typically involves knowing the mean (μ) and standard deviation (σ) of the data set. If these parameters are unknown, they can often be estimated from a sample of data. For instance, the sample mean (x̄) can serve as an estimate of the population mean (μ), and the sample standard deviation (s) can estimate the population standard deviation (σ). Accurate identification of these parameters is critical for the subsequent calculations.
| Parameter | Description | Formula |
|---|---|---|
| Mean (μ) | Central tendency | μ = (Σx)/n |
| Standard Deviation (σ) | Dispersion from the mean | σ = √[(Σ(x-μ)^2)/(n-1)] |

Calculator Operations
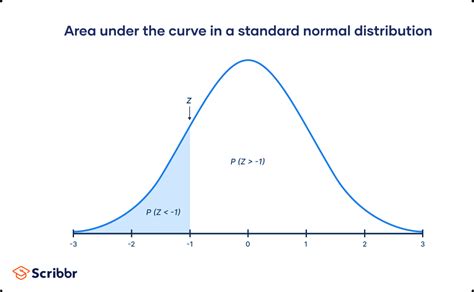
A normal model calculator can perform a variety of operations, including calculating z-scores, finding probabilities (areas under the curve), and determining critical values for hypothesis testing. Understanding the different functions of the calculator and when to apply them is key to effective use.
Tip 2: Calculating Z-Scores
The z-score, which tells you how many standard deviations an element is from the mean, is a fundamental calculation in statistics. The formula for the z-score is z = (X - μ) / σ, where X is the value of the element, μ is the mean of the dataset, and σ is the standard deviation. A normal model calculator can quickly compute z-scores, saving time and reducing the chance of calculation errors.
Tip 3: Finding Probabilities
Another crucial function of a normal model calculator is finding the probability (or area under the curve) for a given range of values. This can be done using z-scores and a standard normal distribution table (z-table) or directly through the calculator if it supports such functionality. Knowing how to find probabilities is essential for hypothesis testing and confidence interval construction.
Interpreting Results
Once you’ve performed calculations with a normal model calculator, the next step is interpreting the results. This involves understanding what the calculated values mean in the context of your data and research question.
Tip 4: Understanding Z-Score Interpretation
A z-score indicates how many standard deviations an observation is away from the mean. A z-score of 0 means the value is equal to the mean. A positive z-score indicates the value is above the mean, while a negative z-score indicates it’s below the mean. The farther the z-score is from 0, the more unusual the value is, assuming a normal distribution.
Tip 5: Contextualizing Probability Results
When finding probabilities, it’s essential to contextualize these results within your research framework. For example, if you’re calculating the probability of observing a value at least as extreme as the one you’ve observed (a p-value), you need to understand what this probability implies about your null hypothesis. Typically, a small p-value (less than a chosen significance level, often 0.05) leads to the rejection of the null hypothesis, suggesting that the observed effect is statistically significant.
Key Points
- Understand the basics of the normal distribution, including mean and standard deviation.
- Accurately identify parameters for calculations, distinguishing between sample and population parameters.
- Familiarize yourself with the operations of a normal model calculator, including z-score calculations and probability findings.
- Correctly interpret calculated z-scores and probabilities in the context of your research question.
- Apply the results of calculator operations to inform statistical decisions, such as hypothesis testing and confidence interval construction.
In conclusion, a normal model calculator is a powerful tool for statistical analysis, offering efficiency and accuracy in calculating probabilities, z-scores, and other parameters related to the normal distribution. By following these tips and understanding the underlying concepts of the normal distribution, you can leverage this tool to enhance your data analysis capabilities, ensuring informed decision-making based on statistical insights.
What is the primary use of a normal model calculator in statistics?
+The primary use of a normal model calculator is to perform calculations related to the normal distribution, such as calculating z-scores, finding probabilities, and determining critical values for hypothesis testing.
How do I choose between sample and population standard deviation formulas?
+The choice between the sample and population standard deviation formulas depends on whether you are working with a sample of data or the entire population. If you’re analyzing a sample, use the sample standard deviation formula. If you have data for the entire population, use the population standard deviation formula.
What does a z-score of 2 indicate?
+A z-score of 2 indicates that the value is 2 standard deviations above the mean. This suggests that the value is relatively unusual, given the normal distribution of the data.