Understanding negative exponents is a crucial aspect of algebra and mathematics in general. Negative exponents are used to represent repeated division by a number, and they follow specific rules that are essential for simplifying expressions and solving equations. The concept of negative exponents can seem daunting at first, but once the rules are grasped, they can be applied with ease to a wide range of mathematical problems. In this article, we will delve into the five key rules for working with negative exponents, providing a comprehensive overview of each rule, along with examples to illustrate their application.
Key Points
- Negative exponents can be converted to positive exponents by taking the reciprocal of the base.
- When multiplying two powers with the same base, the exponents are added, regardless of whether they are positive or negative.
- When dividing two powers with the same base, the exponent of the divisor is subtracted from the exponent of the dividend.
- A negative exponent indicates taking the reciprocal of the expression to change the sign of the exponent.
- When dealing with expressions that involve both positive and negative exponents, simplification often involves combining like terms and applying the rules for adding and subtracting exponents.
Rule 1: Converting Negative Exponents to Positive Exponents

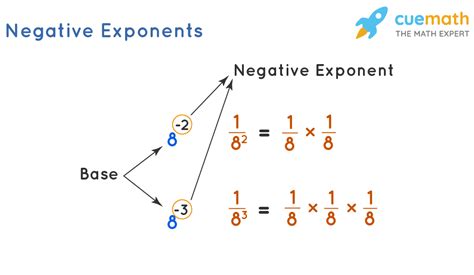
This rule is fundamental in dealing with negative exponents. It states that a^(-n) = 1/a^n, where “a” is the base and “n” is the exponent. Essentially, to convert a negative exponent to a positive one, you take the reciprocal of the base. For example, 2^(-3) = 1⁄2^3 = 1⁄8. This rule helps in simplifying expressions by eliminating negative exponents, making it easier to work with them in equations and other mathematical operations.
Application of Rule 1
The application of this rule is straightforward. Whenever you encounter a negative exponent, you can apply this rule to convert it into a positive exponent by taking the reciprocal of the base. For instance, if you have x^(-2) in an equation, you can rewrite it as 1/x^2, which might make the equation easier to solve or simplify.
Rule 2: Multiplying Powers with the Same Base
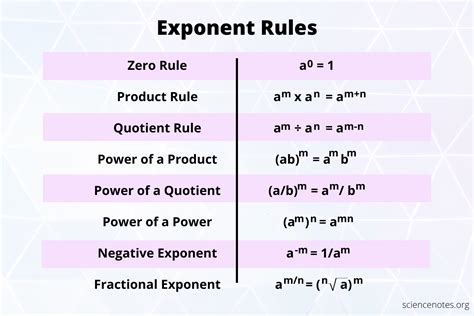
When multiplying two powers that have the same base, you add their exponents. This rule applies regardless of whether the exponents are positive or negative. The formula is a^m * a^n = a^(m+n). For example, 2^3 * 2^(-2) = 2^(3-2) = 2^1 = 2. This rule helps in simplifying expressions that involve the multiplication of powers with the same base.
Example of Rule 2
An example of applying this rule would be simplifying the expression x^4 * x^(-3). Using the rule, we add the exponents: x^(4-3) = x^1 = x. This simplification is crucial in solving algebraic equations and manipulating expressions to find solutions.
Rule 3: Dividing Powers with the Same Base
When dividing two powers with the same base, you subtract the exponent of the divisor from the exponent of the dividend. The formula for this rule is a^m / a^n = a^(m-n). For instance, 2^5 / 2^3 = 2^(5-3) = 2^2 = 4. This rule is essential for simplifying division operations involving powers with the same base.
Application of Rule 3
A practical application of this rule would be in simplifying x^6 / x^4. Applying the rule, we get x^(6-4) = x^2. This simplification can be critical in algebraic manipulations and solving equations where division of powers is involved.
Rule 4: Dealing with Negative Exponents in Expressions
A negative exponent in an expression indicates that you should take the reciprocal of the base to change the sign of the exponent to positive. This means moving the base to the other side of the fraction if it’s not already there. For example, 1/x^(-2) = x^2 because you take the reciprocal of x^(-2) to get x^2. This rule is vital for handling negative exponents in more complex expressions and equations.
Example of Rule 4
An example of applying this rule is when simplifying 1/(x^(-3)). According to the rule, you take the reciprocal, resulting in x^3. This process helps in simplifying complex fractions and expressions that involve negative exponents.
Rule 5: Simplifying Expressions with Both Positive and Negative Exponents

When dealing with expressions that involve both positive and negative exponents, the goal is often to simplify the expression as much as possible. This can involve combining like terms, applying the rules for adding and subtracting exponents, and using the other rules mentioned above to eliminate negative exponents. For instance, x^2 * x^(-3) / x^4 can be simplified by first applying the rule for multiplying powers (x^(2-3) = x^(-1)), then dealing with the division (x^(-1) / x^4 = x^(-1-4) = x^(-5)), and finally applying the rule for negative exponents to simplify further if needed.
Application of Rule 5
A detailed example of applying this rule would involve simplifying x^3 * x^2 / (x^4 * x^(-2)). First, simplify the numerator and denominator separately using the rules for multiplying powers: (x^(3+2)) / (x^(4-2)) = x^5 / x^2. Then, apply the rule for dividing powers: x^(5-2) = x^3. This process demonstrates how to handle complex expressions involving both positive and negative exponents.
| Rule | Description | Example |
|---|---|---|
| 1 | Convert negative to positive exponent | 2^(-3) = 1/2^3 |
| 2 | Multiplying powers with same base | 2^3 * 2^(-2) = 2^(3-2) |
| 3 | Dividing powers with same base | 2^5 / 2^3 = 2^(5-3) |
| 4 | Dealing with negative exponents | 1/x^(-2) = x^2 |
| 5 | Simplifying complex expressions | x^2 * x^(-3) / x^4 |
What is the purpose of negative exponents in mathematics?
+Negative exponents are used to represent repeated division by a number and follow specific rules for simplification and calculation. They are essential in algebra and other mathematical operations for solving equations and simplifying expressions.
How do you convert a negative exponent to a positive one?
+To convert a negative exponent to a positive one, you take the reciprocal of the base. For example, a^(-n) = 1/a^n. This rule is fundamental in dealing with negative exponents and simplifying expressions.
What is the difference between multiplying and dividing powers with the same base?
+When multiplying powers with the same base, you add their exponents. When dividing powers with the same base, you subtract the exponent of the divisor from the exponent of the dividend. These rules are crucial for simplifying expressions involving powers with the same base.
In conclusion, understanding and applying the rules for negative exponents is crucial for mathematical operations involving powers and exponents. By mastering these rules, individuals can simplify complex expressions, solve equations, and tackle more advanced mathematical concepts with confidence. Remember, practice is key to becoming proficient in working with negative exponents, so continue to apply these rules in various mathematical contexts to reinforce your understanding.