The multiplication property of equality is a fundamental concept in mathematics, specifically in algebra, that enables us to solve equations by multiplying both sides of the equation by the same value. This property is based on the principle that if two quantities are equal, then multiplying them by the same non-zero value will result in equal products. In essence, if $a = b$, then $ac = bc$ for any non-zero value of $c$. This concept is crucial for simplifying and solving linear equations, which are equations in which the highest power of the variable (usually $x$) is 1.
Understanding the multiplication property of equality is essential for algebraic manipulations, as it allows us to isolate variables, simplify expressions, and solve for unknowns in a systematic and logical manner. The property can be applied in various mathematical contexts, including solving linear equations, graphing lines, and manipulating algebraic expressions. Its application extends beyond basic algebra, influencing more advanced mathematical disciplines such as calculus, geometry, and trigonometry.
Key Points
- The multiplication property of equality states that if $a = b$, then $ac = bc$ for any non-zero value of $c$.
- This property is fundamental for solving linear equations and simplifying algebraic expressions.
- It allows for the isolation of variables and the solution of equations in a systematic way.
- Application of the property requires careful consideration to avoid multiplying by zero, as this would invalidate the equation.
- The property is a cornerstone of algebraic manipulations and has implications in various mathematical disciplines beyond basic algebra.
Applying the Multiplication Property of Equality
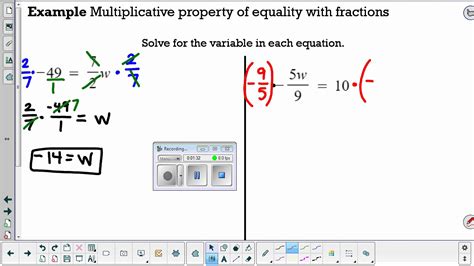
When applying the multiplication property of equality, it is crucial to ensure that the same operation is performed on both sides of the equation. This maintains the balance of the equation and ensures that the solution set remains unchanged. For instance, if we have the equation x = 5 and we multiply both sides by 3, we get 3x = 15. This application is straightforward and demonstrates how the property can be used to generate equivalent equations.
A more nuanced application involves using the multiplication property to solve equations involving fractions. For example, given the equation $\frac{x}{4} = 9$, we can multiply both sides by 4 to isolate $x$, resulting in $x = 36$. This example illustrates how the property can be used to eliminate fractions and simplify equations, making it easier to solve for the variable.
Considerations and Limitations
While the multiplication property of equality is a powerful tool for solving equations, there are considerations and limitations to its application. One critical aspect is the avoidance of multiplying by zero. If we were to multiply both sides of an equation by zero, we would essentially be stating that 0 = 0, regardless of the original equation’s validity. This would lead to a loss of information and potentially incorrect conclusions. Therefore, it is essential to ensure that the multiplier is non-zero when applying the multiplication property.
| Operation | Equation | Result |
|---|---|---|
| Multiplication by 3 | $x = 5$ | $3x = 15$ |
| Multiplication by 4 | $\frac{x}{4} = 9$ | $x = 36$ |
| Multiplication by 0 | $a = b$ | Invalidates the equation |

Conclusion and Future Directions

In conclusion, the multiplication property of equality is a foundational concept in algebra that enables the systematic solution of linear equations. Its application, considerations, and limitations have been discussed, highlighting its importance and the need for careful handling to avoid common pitfalls such as multiplication by zero. As mathematics continues to evolve, understanding and applying the multiplication property of equality will remain essential for advancing in various mathematical disciplines and solving complex problems.
What is the multiplication property of equality?
+The multiplication property of equality states that if a = b, then ac = bc for any non-zero value of c. This means that if two quantities are equal, multiplying them by the same non-zero value will result in equal products.
Why is the multiplication property of equality important?
+The multiplication property of equality is important because it allows us to solve linear equations and simplify algebraic expressions in a systematic way. It is a fundamental concept in algebra and has applications in various mathematical disciplines.
Can you multiply both sides of an equation by zero?
+No, multiplying both sides of an equation by zero is not valid because it would result in 0 = 0, regardless of the original equation’s validity, leading to a loss of information and potentially incorrect conclusions.



