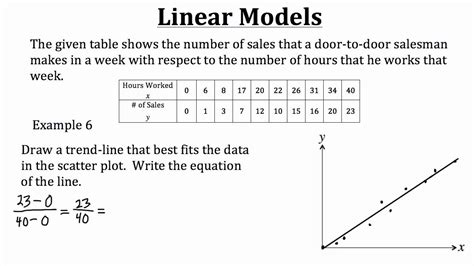
Linear models are a fundamental component of machine learning and statistical analysis, used for predicting outcomes based on one or more predictor variables. These models assume a linear relationship between the predictors and the response variable, making them widely applicable but also susceptible to issues like non-linearity and multicollinearity. To effectively work with linear models, it's essential to understand their underlying principles and how to address common challenges. Here are five tips to enhance your work with linear models, ensuring they are as effective and reliable as possible.
Key Points
- Understand the assumptions of linear models to ensure their validity.
- Feature engineering can significantly improve model performance by creating relevant predictors.
- Regularization techniques help in preventing overfitting by controlling model complexity.
- Model evaluation metrics should be chosen based on the problem's context and requirements.
- Interpretation of coefficients and predictions requires careful consideration of the data's scale and context.
Understanding Linear Model Assumptions
Linear models rely on several assumptions, including linearity, independence, homoscedasticity, normality, and no multicollinearity. Violations of these assumptions can lead to inaccurate predictions and misleading conclusions. For instance, non-linearity can be addressed through transformations of the variables or using polynomial terms, while homoscedasticity issues might require the use of generalized linear models or transformation of the response variable. Understanding and checking these assumptions are crucial steps in the model development process.
Feature Engineering for Enhanced Prediction
Feature engineering involves selecting and transforming raw data into features that are more suitable for modeling. This process can significantly improve the performance of linear models by capturing non-linear relationships, interactions between variables, or by reducing the dimensionality of the data. Techniques such as polynomial regression, interaction terms, and principal component analysis (PCA) can be useful in creating a more informative set of predictors. For example, in a model predicting house prices, including features like the number of bedrooms, square footage, and location can provide a more accurate prediction than using just one or two of these variables.
| Feature Engineering Technique | Description |
|---|---|
| Polynomial Regression | Incorporates non-linear relationships by adding polynomial terms of the predictors. |
| Interaction Terms | Accounts for the interaction effects between different predictor variables. |
| Principal Component Analysis (PCA) | Reduces dimensionality by transforming correlated variables into a set of uncorrelated components. |
Regularization Techniques for Model Improvement
Regularization techniques, such as Lasso (L1 regularization) and Ridge (L2 regularization), are used to prevent overfitting by adding a penalty term to the loss function. This penalty term discourages large weights, thereby reducing the model’s capacity to fit the noise in the training data. Lasso regression can also be used for feature selection, as it sets the coefficients of non-important features to zero. The choice between Lasso and Ridge depends on the specific problem; if feature selection is a priority, Lasso might be preferred, while Ridge is more suitable when all predictors are believed to be important.
Model Evaluation Metrics
The choice of evaluation metrics for linear models depends on the problem’s context. For continuous outcomes, metrics like Mean Squared Error (MSE), Mean Absolute Error (MAE), and R-squared are commonly used. MSE measures the average squared difference between predicted and actual values, MAE measures the average absolute difference, and R-squared indicates the proportion of the variance in the response variable that is predictable from the predictor variables. For classification problems, metrics such as accuracy, precision, recall, and F1 score are more appropriate. It’s also crucial to evaluate models using techniques like cross-validation to get a more realistic estimate of their performance on unseen data.
Interpreting Coefficients and Predictions
Interpreting the coefficients of a linear model involves understanding the change in the response variable for a one-unit change in the predictor variable, while holding all other predictors constant. The scale of the variables can affect this interpretation; for instance, a coefficient of 2 for a predictor that ranges from 0 to 100 has a different practical significance than the same coefficient for a predictor that ranges from 0 to 1. Furthermore, predictions should be interpreted within the context of the data’s scale and the model’s assumptions, considering factors like the range of the predictor variables and the potential for extrapolation beyond the observed data range.
What is the primary assumption of linear regression regarding the relationship between predictors and the response variable?
+The primary assumption is that the relationship between the predictors and the response variable is linear. This means that as the value of a predictor increases, the value of the response variable changes at a constant rate, assuming all other predictors are held constant.
How does regularization help in improving the performance of linear models?
+Regularization helps by adding a penalty term to the loss function, which discourages large weights and thereby reduces the risk of overfitting. This makes the model more generalizable to new, unseen data.
What is the difference between Lasso and Ridge regression in terms of their application?
+Lasso (L1 regularization) can set the coefficients of non-important features to zero, effectively performing feature selection. Ridge (L2 regularization) reduces the magnitude of all coefficients but does not set any to zero. The choice between them depends on whether feature selection is a priority.
In conclusion, working effectively with linear models requires a deep understanding of their assumptions, the ability to engineer informative features, knowledge of regularization techniques, the appropriate selection of evaluation metrics, and careful interpretation of coefficients and predictions. By mastering these aspects, professionals can harness the full potential of linear models to solve complex problems in a wide range of fields, from economics and finance to engineering and healthcare.