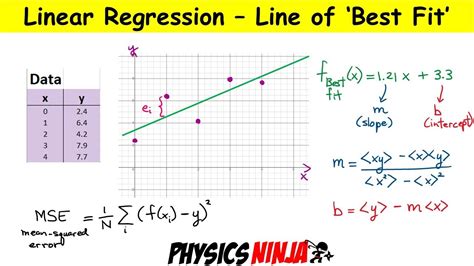
The best fit formula, also known as linear regression, is a statistical method used to create a linear equation that best predicts the value of a dependent variable based on one or more independent variables. The goal of the best fit formula is to find the line that minimizes the sum of the squared errors between the observed data points and the predicted values. In this article, we will explore five ways to apply the best fit formula in real-world scenarios, including its application in data analysis, predictive modeling, and business decision-making.
Key Points
- The best fit formula is a statistical method used to create a linear equation that best predicts the value of a dependent variable.
- The goal of the best fit formula is to find the line that minimizes the sum of the squared errors between the observed data points and the predicted values.
- The best fit formula has numerous applications in data analysis, predictive modeling, and business decision-making.
- It can be used to analyze the relationship between two or more variables, identify trends and patterns, and make predictions about future outcomes.
- The best fit formula can be applied in various fields, including economics, finance, engineering, and social sciences.
Method 1: Simple Linear Regression
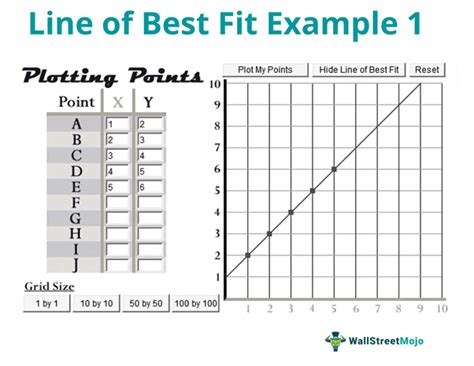
Simple linear regression is a statistical method that involves creating a linear equation to predict the value of a dependent variable based on one independent variable. The equation takes the form of Y = a + bX, where Y is the dependent variable, X is the independent variable, a is the intercept, and b is the slope. The best fit formula is used to find the values of a and b that minimize the sum of the squared errors between the observed data points and the predicted values.
Example: Predicting House Prices
Suppose we want to predict the price of a house based on its size. We collect data on the size of several houses and their corresponding prices. Using the best fit formula, we can create a linear equation that predicts the price of a house based on its size. For example, if the equation is Y = 200,000 + 100X, where X is the size of the house in square feet, we can predict the price of a house that is 2,000 square feet in size.
| House Size (X) | House Price (Y) |
|---|---|
| 1,500 | 250,000 |
| 2,000 | 300,000 |
| 2,500 | 350,000 |
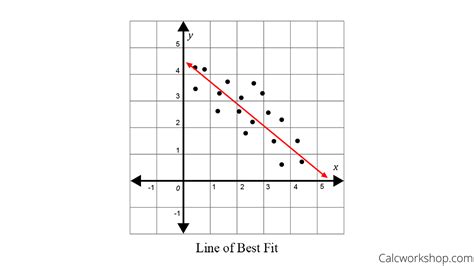
Method 2: Multiple Linear Regression
Multiple linear regression is a statistical method that involves creating a linear equation to predict the value of a dependent variable based on two or more independent variables. The equation takes the form of Y = a + b1X1 + b2X2 + … + bnXn, where Y is the dependent variable, X1, X2, …, Xn are the independent variables, a is the intercept, and b1, b2, …, bn are the slopes. The best fit formula is used to find the values of a, b1, b2, …, bn that minimize the sum of the squared errors between the observed data points and the predicted values.
Example: Predicting Stock Prices
Suppose we want to predict the price of a stock based on several factors, including the company’s revenue, earnings per share, and dividend yield. We collect data on these factors and the corresponding stock prices. Using the best fit formula, we can create a linear equation that predicts the stock price based on these factors. For example, if the equation is Y = 50 + 0.5X1 + 0.2X2 + 0.1X3, where X1 is the revenue, X2 is the earnings per share, and X3 is the dividend yield, we can predict the stock price based on these factors.
Method 3: Polynomial Regression
Polynomial regression is a statistical method that involves creating a non-linear equation to predict the value of a dependent variable based on one or more independent variables. The equation takes the form of Y = a + b1X + b2X^2 + … + bnX^n, where Y is the dependent variable, X is the independent variable, a is the intercept, and b1, b2, …, bn are the coefficients. The best fit formula is used to find the values of a, b1, b2, …, bn that minimize the sum of the squared errors between the observed data points and the predicted values.
Example: Predicting Customer Satisfaction
Suppose we want to predict customer satisfaction based on the quality of a product. We collect data on the quality of the product and the corresponding customer satisfaction ratings. Using the best fit formula, we can create a non-linear equation that predicts customer satisfaction based on the quality of the product. For example, if the equation is Y = 50 + 10X - 0.5X^2, where X is the quality of the product, we can predict customer satisfaction based on the quality of the product.
Method 4: Logistic Regression
Logistic regression is a statistical method that involves creating a non-linear equation to predict the probability of a dependent variable based on one or more independent variables. The equation takes the form of P(Y=1) = 1 / (1 + e^(-z)), where P(Y=1) is the probability of the dependent variable, z is a linear combination of the independent variables, and e is the base of the natural logarithm. The best fit formula is used to find the values of the coefficients that minimize the sum of the squared errors between the observed data points and the predicted probabilities.
Example: Predicting Credit Risk
Suppose we want to predict the probability of default based on several factors, including the borrower’s credit score, income, and debt-to-income ratio. We collect data on these factors and the corresponding default outcomes. Using the best fit formula, we can create a non-linear equation that predicts the probability of default based on these factors. For example, if the equation is P(Y=1) = 1 / (1 + e^(-z)), where z = 0.5X1 + 0.2X2 + 0.1X3, and X1 is the credit score, X2 is the income, and X3 is the debt-to-income ratio, we can predict the probability of default based on these factors.
Method 5: Ridge Regression

Ridge regression is a statistical method that involves creating a linear equation to predict the value of a dependent variable based on one or more independent variables, with a penalty term added to the cost function to prevent overfitting. The equation takes the form of Y = a + b1X1 + b2X2 + … + bnXn, where Y is the dependent variable, X1, X2, …, Xn are the independent variables, a is the intercept, and b1, b2, …, bn are the slopes. The best fit formula is used to find the values of a, b1, b2, …, bn that minimize the sum of the squared errors between the observed data points and the predicted values, subject to a penalty term that prevents the coefficients from becoming too large.
Example: Predicting Energy Consumption
Suppose we want to predict energy consumption based on several factors, including the temperature, humidity, and wind speed. We collect data on these factors and the corresponding energy consumption values. Using the best fit formula, we can create a linear equation that predicts energy consumption based on these factors, with a penalty term added to prevent overfitting. For example, if the equation is Y = 100 + 0.5X1 + 0.2X2 + 0.1X3, where X1 is the temperature, X2 is the humidity, and X3 is the wind speed, we can predict energy consumption based on these factors.
What is the best fit formula?
+The best fit formula is a statistical method used to create a linear equation that best predicts the value of a dependent variable based on one or more independent variables.
What are the applications of the best fit formula?
+The best fit formula has numerous applications in data analysis, predictive modeling, and business decision-making, including predicting house prices, stock prices, customer satisfaction, credit risk, and energy consumption.
How is the best fit formula used in predictive modeling?
+The best fit formula is used in predictive modeling to create a linear equation that predicts the value of a dependent variable based on one or more independent variables, and to identify the most important factors that affect the dependent variable.