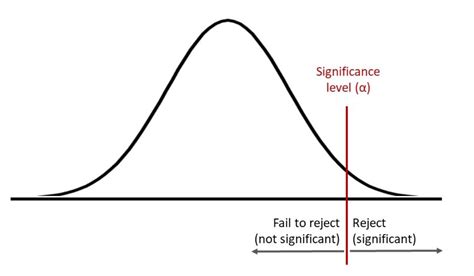
The concept of level of significance is a fundamental principle in statistical hypothesis testing, which plays a crucial role in determining the validity of a research study's findings. In essence, the level of significance, often denoted as alpha (α), represents the maximum probability of rejecting a true null hypothesis, thereby committing a Type I error. This error occurs when a researcher incorrectly concludes that an observed effect or relationship is statistically significant, whereas, in reality, it is due to chance. The level of significance is typically set before conducting a study, and common values for alpha include 0.05, 0.01, and 0.001, with 0.05 being the most commonly used threshold in social sciences and biological research.
Understanding the Concept of Level of Significance

To grasp the level of significance fully, it’s essential to understand its relationship with the p-value, which is a statistical measure that calculates the probability of observing the results, or more extreme, if the null hypothesis is true. The p-value serves as a critical component in hypothesis testing, as it helps researchers determine whether their findings are statistically significant. When the p-value is less than the predetermined level of significance (alpha), the null hypothesis is rejected, indicating that the observed effect is statistically significant. Conversely, if the p-value is greater than alpha, the null hypothesis is failed to be rejected, suggesting that the observed effect may be due to chance.
Importance of Level of Significance in Research
The level of significance holds substantial importance in research, as it directly impacts the interpretation of study results. By setting a stringent level of significance, researchers can increase the confidence in their findings, ensuring that the observed effects are not merely the result of random chance. However, an overly conservative alpha level may lead to Type II errors, where a real effect is missed. Therefore, the choice of alpha level should be carefully considered, taking into account the research question, study design, and potential consequences of false positives or false negatives.
| Alpha Level | Type I Error Rate | Common Usage |
|---|---|---|
| 0.05 | 5% | Social sciences, biological research |
| 0.01 | 1% | Medical research, high-stakes decisions |
| 0.001 | 0.1% | Critical applications, high-risk fields |

Statistical Hypothesis Testing and Level of Significance
Statistical hypothesis testing is a systematic procedure used to evaluate the validity of a research hypothesis. This process involves formulating a null and alternative hypothesis, selecting a sample, calculating the test statistic, and determining the p-value. The level of significance is crucial in this process, as it serves as the threshold for determining statistical significance. By comparing the p-value to the predetermined alpha level, researchers can decide whether to reject the null hypothesis, thereby supporting the research hypothesis.
Common Misconceptions About Level of Significance
Several misconceptions surround the concept of level of significance. One common mistake is believing that the level of significance directly reflects the probability of the null hypothesis being true. However, the alpha level only represents the maximum probability of committing a Type I error, not the probability of the null hypothesis itself. Another misconception is that a low p-value (e.g., 0.001) necessarily implies a large or practically significant effect. In reality, the p-value only indicates the probability of observing the results, or more extreme, assuming the null hypothesis is true, and does not provide information about the effect size.
Key Points
- The level of significance (alpha) represents the maximum probability of rejecting a true null hypothesis.
- The p-value is a statistical measure that calculates the probability of observing the results, or more extreme, if the null hypothesis is true.
- The choice of alpha level should be carefully considered, taking into account the research question, study design, and potential consequences of false positives or false negatives.
- A low p-value does not necessarily imply a large or practically significant effect.
- The level of significance is not a fixed value and can be adjusted based on the research context.
Practical Applications of Level of Significance
The concept of level of significance has far-reaching implications in various fields, including medicine, social sciences, and business. In medical research, the level of significance is crucial in evaluating the efficacy of new treatments or drugs. For instance, a study investigating the effectiveness of a new medication may use a stringent alpha level (e.g., 0.01) to minimize the risk of false positives, which could have severe consequences. In social sciences, researchers may use a more liberal alpha level (e.g., 0.05) to detect subtle effects or relationships. In business, the level of significance is essential in evaluating the effectiveness of marketing campaigns or financial investments.
Future Directions and Emerging Trends
As research methods and statistical techniques continue to evolve, the concept of level of significance will remain a vital component of statistical hypothesis testing. Emerging trends, such as the use of Bayesian methods and machine learning algorithms, may challenge traditional notions of level of significance and p-values. However, the fundamental principles of hypothesis testing and the importance of carefully considering the level of significance will remain unchanged. By understanding the level of significance and its role in statistical hypothesis testing, researchers can ensure that their findings are reliable, valid, and contribute meaningfully to their respective fields.
What is the purpose of setting a level of significance in statistical hypothesis testing?
+The purpose of setting a level of significance is to determine the maximum probability of committing a Type I error, thereby ensuring that the observed effects are not merely the result of random chance.
How does the level of significance relate to the p-value?
+The p-value is a statistical measure that calculates the probability of observing the results, or more extreme, if the null hypothesis is true. When the p-value is less than the predetermined level of significance (alpha), the null hypothesis is rejected, indicating that the observed effect is statistically significant.
What are the implications of setting a high or low level of significance?
+A high level of significance (e.g., 0.05) may increase the risk of false positives, while a low level of significance (e.g., 0.01) may increase the risk of false negatives. The choice of alpha level should be carefully considered, taking into account the research question, study design, and potential consequences of false positives or false negatives.