The concept of total probability is a fundamental principle in probability theory, allowing us to calculate the probability of an event by considering all possible outcomes and their respective probabilities. This principle is widely applied in various fields, including statistics, engineering, economics, and computer science. In this article, we will explore five ways the total probability theorem can be utilized, highlighting its importance and versatility in problem-solving.
Introduction to Total Probability Theorem
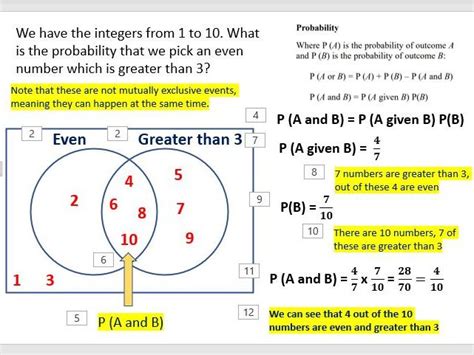
The total probability theorem states that if we have a set of mutually exclusive events {A1, A2,…, An} whose union is the sample space S, then for any event B, the probability of B can be calculated as the sum of the probabilities of B given each of the events A1, A2,…, An, weighted by the probability of each event. Mathematically, this can be expressed as P(B) = ∑[P(B|Ai) * P(Ai)]. This theorem provides a powerful tool for calculating probabilities in complex scenarios by breaking them down into more manageable parts.
Key Points
- The total probability theorem allows for the calculation of the probability of an event by considering all possible outcomes and their respective probabilities.
- It is applicable in various fields, including statistics, engineering, economics, and computer science.
- The theorem can be used for decision-making under uncertainty by evaluating the probability of different outcomes.
- It facilitates the calculation of conditional probabilities, which are essential in Bayesian inference and machine learning.
- The total probability theorem is useful in risk analysis, enabling the assessment of the likelihood of adverse events.
Application in Decision-Making Under Uncertainty
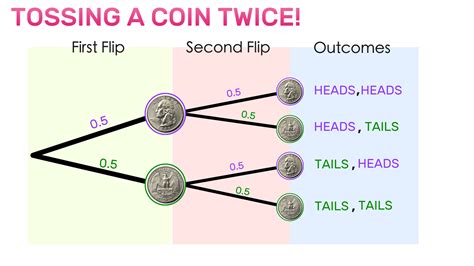
One of the significant applications of the total probability theorem is in decision-making under uncertainty. In real-world scenarios, decisions often involve uncertainty about the outcomes of different actions. By applying the total probability theorem, decision-makers can evaluate the probability of different outcomes and make informed decisions based on these probabilities. For instance, in business, the theorem can be used to assess the potential returns on investment under different market conditions, helping executives make strategic decisions.
Calculating Conditional Probabilities
The total probability theorem is also crucial in calculating conditional probabilities, which are probabilities of an event occurring given that another event has occurred. Conditional probabilities are fundamental in Bayesian inference, a statistical framework used for updating the probability of a hypothesis based on new evidence. The theorem enables the calculation of these probabilities by considering all possible scenarios and their respective probabilities, making it an indispensable tool in machine learning and artificial intelligence.
| Application Area | Role of Total Probability Theorem |
|---|---|
| Decision-Making | Evaluating the probability of different outcomes under uncertainty |
| Conditional Probability Calculation | Calculating probabilities of events given that other events have occurred |
| Risk Analysis | Assessing the likelihood of adverse events |
| Machine Learning | Updating probabilities of hypotheses based on new evidence in Bayesian inference |
| Engineering | Designing systems that can operate under various conditions with known probabilities |

Risk Analysis and Management
The total probability theorem plays a critical role in risk analysis and management. By calculating the probability of adverse events, organizations can better prepare for potential risks and develop strategies to mitigate them. This is particularly important in fields like finance, where the ability to assess and manage risk can significantly impact an institution’s stability and profitability. The theorem helps in quantifying risks, enabling more accurate risk assessment and the implementation of appropriate risk management strategies.
Engineering Applications
In engineering, the total probability theorem is used in the design and operation of systems that must function under a variety of conditions, each with its own probability of occurrence. For example, in the design of electronic circuits, engineers must consider the probability of component failures and the overall system reliability. The theorem helps in calculating these probabilities, ensuring that systems are designed to meet specific reliability standards and can operate effectively under various conditions.
In conclusion, the total probability theorem is a foundational principle in probability theory with far-reaching applications across different disciplines. Its ability to facilitate the calculation of probabilities under uncertainty makes it an essential tool in decision-making, risk analysis, machine learning, and engineering. As the complexity of systems and the uncertainty of outcomes continue to increase, the importance of the total probability theorem in providing a framework for understanding and managing uncertainty will only continue to grow.
What is the total probability theorem?
+The total probability theorem is a principle in probability theory that allows for the calculation of the probability of an event by considering all possible outcomes and their respective probabilities.
Where is the total probability theorem applied?
+The theorem is applied in various fields, including statistics, engineering, economics, computer science, and decision-making under uncertainty.
What is the role of the total probability theorem in risk analysis?
+The theorem plays a critical role in risk analysis by enabling the calculation of the probability of adverse events, thus helping in the development of strategies to mitigate these risks.



