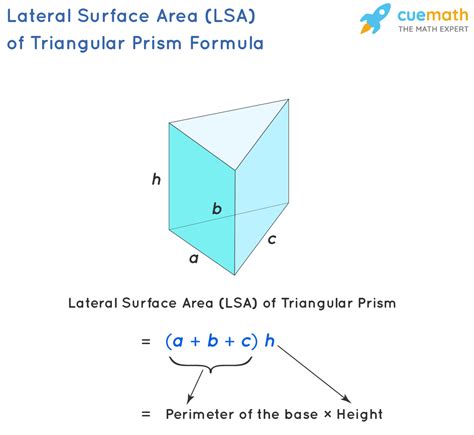
The lateral surface area of a triangular prism is a fundamental concept in geometry, essential for calculating the total surface area of the prism. A triangular prism is a three-dimensional solid object with two identical faces that are triangles, and three rectangular faces connecting them. To understand the lateral surface area, it's crucial to first grasp the basic components of the prism and how they contribute to its overall surface area.
Key Points
- The lateral surface area of a triangular prism is the sum of the areas of its three rectangular faces.
- The formula for the lateral surface area (LSA) is LSA = h(a + b + c), where h is the height of the prism, and a, b, and c are the lengths of the sides of the triangular base.
- The total surface area (TSA) of the prism includes the areas of the two triangular bases in addition to the lateral surface area, given by TSA = LSA + 2 × (Area of the triangular base).
- Understanding the dimensions and geometry of the triangular prism is essential for accurately calculating its lateral and total surface areas.
- Applications of these calculations are found in various fields, including architecture, engineering, and design, where precise measurements of surface areas are critical.
Calculating Lateral Surface Area

To calculate the lateral surface area of a triangular prism, one must consider the dimensions of the prism, specifically the height and the lengths of the sides of the triangular base. The formula for the lateral surface area, LSA = h(a + b + c), directly reflects these dimensions, where h is the height of the prism, and a, b, and c are the lengths of the sides of the triangular base.
Formula Breakdown and Application
The formula LSA = h(a + b + c) can be applied by substituting the known values of h, a, b, and c. For instance, if the height h of the prism is 5 units, and the sides of the triangular base are 3 units, 4 units, and 5 units, the lateral surface area would be LSA = 5(3 + 4 + 5) = 5 × 12 = 60 square units.
| Dimension | Value |
|---|---|
| Height (h) | 5 units |
| Sides of the triangular base (a, b, c) | 3 units, 4 units, 5 units |
| Lateral Surface Area (LSA) | 60 square units |

Practical Applications and Considerations
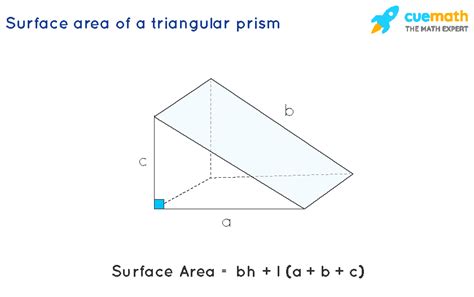
The calculation of the lateral surface area of a triangular prism has numerous practical applications. In architecture, for example, understanding the surface areas of structures is vital for estimating material costs and ensuring structural integrity. Similarly, in engineering and design, precise calculations of surface areas are necessary for optimizing the performance and efficiency of systems and products.
Challenges and Limitations
While the formula for the lateral surface area provides a straightforward method for calculation, challenges can arise when dealing with complex or irregularly shaped triangular prisms. In such cases, breaking down the prism into simpler geometric shapes or using advanced mathematical techniques may be necessary to accurately determine the surface area.
In conclusion, the lateral surface area of a triangular prism is a fundamental concept that requires a solid understanding of the prism's geometry and dimensions. By applying the formula LSA = h(a + b + c) and considering the practical applications and potential challenges, individuals can accurately calculate the lateral surface area and contribute to a wide range of fields and projects.
What is the formula for the lateral surface area of a triangular prism?
+The formula for the lateral surface area (LSA) of a triangular prism is LSA = h(a + b + c), where h is the height of the prism, and a, b, and c are the lengths of the sides of the triangular base.
How do you calculate the total surface area of a triangular prism?
+The total surface area (TSA) of a triangular prism is calculated by adding the lateral surface area to twice the area of the triangular base, given by TSA = LSA + 2 × (Area of the triangular base).
What are some practical applications of calculating the lateral surface area of a triangular prism?
+Practical applications include estimating material costs in architecture, optimizing performance in engineering, and designing efficient systems and products. Precise calculations of surface areas are critical in these fields for ensuring structural integrity and efficiency.