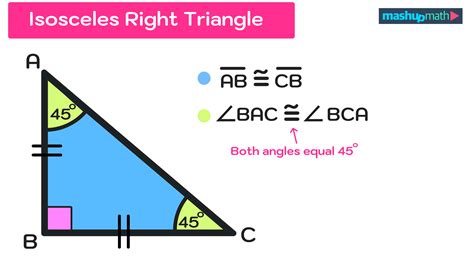
The isosceles right triangle is a fundamental concept in geometry, characterized by two sides of equal length and a right angle. Understanding the properties and applications of this triangle is crucial for various fields, including architecture, engineering, and design. Here are five key facts about the isosceles right triangle, providing insight into its unique characteristics and uses.
Key Points
- The isosceles right triangle has two sides of equal length, which meet at a right angle (90 degrees).
- The triangle's two equal sides are referred to as legs, while the side opposite the right angle is called the hypotenuse.
- The isosceles right triangle has a specific ratio of side lengths, with the hypotenuse being √2 times the length of each leg.
- This triangle is often used in construction and design due to its unique properties, such as its ability to form a square when two triangles are combined.
- The isosceles right triangle plays a significant role in trigonometry, as it helps to define the values of sine, cosine, and tangent for 45-degree angles.
Properties of the Isosceles Right Triangle
The isosceles right triangle is defined by its two equal sides, which are typically denoted as legs, and the hypotenuse, which is the side opposite the right angle. The triangle’s right angle is 90 degrees, while the other two angles are each 45 degrees. This unique combination of angles and side lengths gives the isosceles right triangle its distinct properties and makes it a fundamental building block in various geometric constructions.
Side Length Ratios and the Pythagorean Theorem
A key characteristic of the isosceles right triangle is the relationship between its side lengths. According to the Pythagorean theorem, in a right-angled triangle, the square of the length of the hypotenuse © is equal to the sum of the squares of the other two sides (a and b), or a^2 + b^2 = c^2. For an isosceles right triangle, since the two legs (a and b) are equal, we can say that a = b. Therefore, the equation simplifies to a^2 + a^2 = c^2, or 2a^2 = c^2. Taking the square root of both sides gives us c = √2 * a, showing that the hypotenuse is √2 times the length of each leg.
| Side | Length Relationship |
|---|---|
| Legs (a and b) | a = b |
| Hypotenuse (c) | c = √2 * a |
Applications of the Isosceles Right Triangle
The isosceles right triangle has numerous applications across various fields, including architecture, engineering, and design. Its unique properties make it an ideal shape for constructing squares, rectangles, and other geometric figures. In construction, the isosceles right triangle is used to ensure that buildings and structures are properly aligned and symmetrical. Additionally, the triangle’s properties are essential in trigonometry for defining the values of sine, cosine, and tangent for 45-degree angles, which are critical in calculations involving right-angled triangles.
Trigonometric Applications
In trigonometry, the isosceles right triangle plays a pivotal role in defining the sine, cosine, and tangent of 45-degree angles. Since the triangle has two 45-degree angles and one 90-degree angle, and the sides opposite and adjacent to the 45-degree angles are equal, we can determine that the sine and cosine of 45 degrees are both 1/√2. The tangent of 45 degrees is 1, as the ratio of the opposite side to the adjacent side is 1:1. These values are fundamental in trigonometric calculations and are used extensively in physics, engineering, and other fields.
What is the relationship between the sides of an isosceles right triangle?
+In an isosceles right triangle, the two legs are of equal length, and the hypotenuse is √2 times the length of each leg.
What are the angles of an isosceles right triangle?
+The isosceles right triangle has two 45-degree angles and one 90-degree angle.
What is the significance of the isosceles right triangle in trigonometry?
+The isosceles right triangle is used to define the values of sine, cosine, and tangent for 45-degree angles, which are essential in trigonometric calculations.
In conclusion, the isosceles right triangle is a geometric figure with unique properties and applications. Its equal sides and right angle make it a fundamental shape in geometry and trigonometry, with applications in various fields. Understanding the isosceles right triangle’s characteristics, such as its side length ratios and trigonometric values, is essential for solving problems and constructing geometric figures. As demonstrated, the isosceles right triangle plays a pivotal role in defining key trigonometric values and is a crucial component in the construction of various geometric shapes and structures.