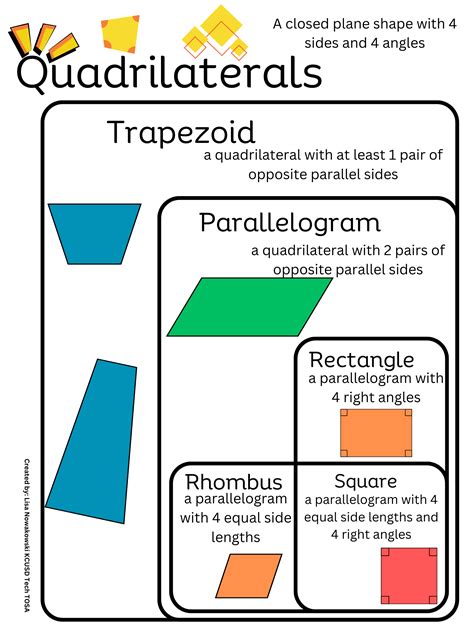
The question of whether a trapezoid is a parallelogram is a common point of discussion in geometry. To address this, let's first define both terms. A trapezoid is a quadrilateral with at least one pair of parallel sides, while a parallelogram is a quadrilateral with two pairs of parallel sides. Given these definitions, it's clear that not all trapezoids meet the criteria for being parallelograms since a trapezoid only requires one pair of parallel sides.
Definition and Characteristics
A deeper look into the characteristics of both shapes reveals key differences. A parallelogram has opposite sides that are not only parallel but also equal in length. Additionally, the opposite angles of a parallelogram are equal, and the sum of two adjacent angles is 180 degrees. In contrast, a trapezoid does not have these specific constraints on its sides or angles, other than having at least one pair of parallel sides.
Comparison of Properties
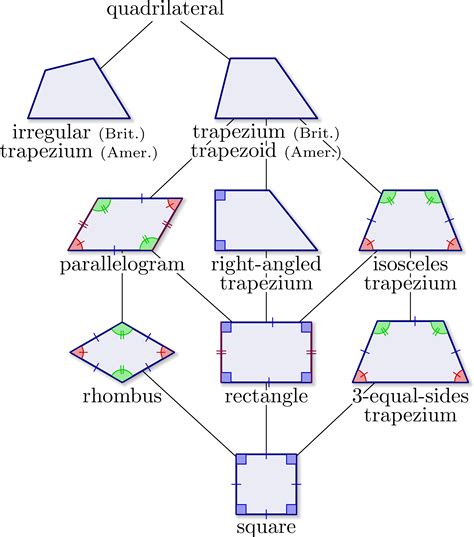
When comparing the properties of trapezoids and parallelograms, it becomes evident that while all parallelograms can be considered trapezoids (since they all have at least one pair of parallel sides), not all trapezoids are parallelograms. This is because the definition of a parallelogram is more restrictive, requiring two pairs of parallel sides. The properties of parallelograms, such as equal opposite sides and angles, are not inherent to all trapezoids.
| Shape | Parallel Sides | Opposite Sides Equal | Opposite Angles Equal |
|---|---|---|---|
| Parallelogram | 2 pairs | Yes | Yes |
| Trapezoid | At least 1 pair | No | No |
Key Points
- A trapezoid is defined as a quadrilateral with at least one pair of parallel sides.
- A parallelogram is a quadrilateral with two pairs of parallel sides and equal opposite sides and angles.
- Not all trapezoids are parallelograms, but all parallelograms can be considered trapezoids.
- The properties of parallelograms, such as equal opposite sides and angles, do not apply to all trapezoids.
- Understanding the differences between trapezoids and parallelograms is essential for geometric analysis and problem-solving.
Given the distinct definitions and properties of trapezoids and parallelograms, it's clear that while there is some overlap in their characteristics, they are not interchangeable terms. Each has its unique set of properties that distinguish it from other geometric shapes. The understanding and application of these properties are fundamental to geometry and are used in a wide range of mathematical and real-world problems.
Meta Description: Explore the definitions and properties of trapezoids and parallelograms, understanding their differences and similarities, and how these distinctions impact geometric analysis and problem-solving.
What is the primary difference between a trapezoid and a parallelogram?
+The primary difference lies in the number of parallel sides: a trapezoid has at least one pair, while a parallelogram has two pairs of parallel sides.
Can all trapezoids be considered parallelograms?
+No, not all trapezoids can be considered parallelograms because they do not all meet the criteria of having two pairs of parallel sides.
What are some key properties of parallelograms that distinguish them from trapezoids?
+Parallelograms have equal opposite sides and angles, and the sum of two adjacent angles is 180 degrees, properties not inherent to all trapezoids.