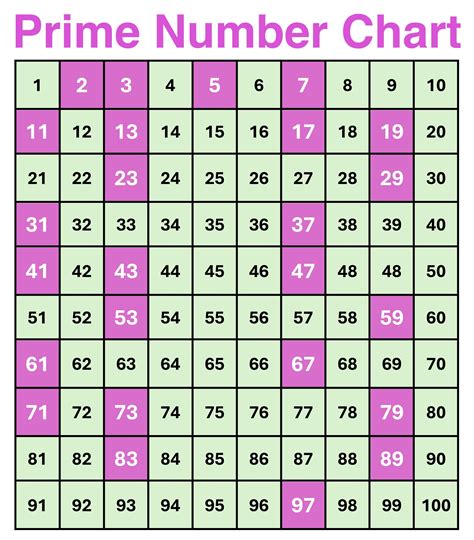
To determine if 29 is a prime number, we need to understand what prime numbers are. Prime numbers are positive integers greater than 1 that have no positive integer divisors other than 1 and themselves. In other words, the only factors of a prime number are 1 and the number itself.
Definition and Characteristics of Prime Numbers
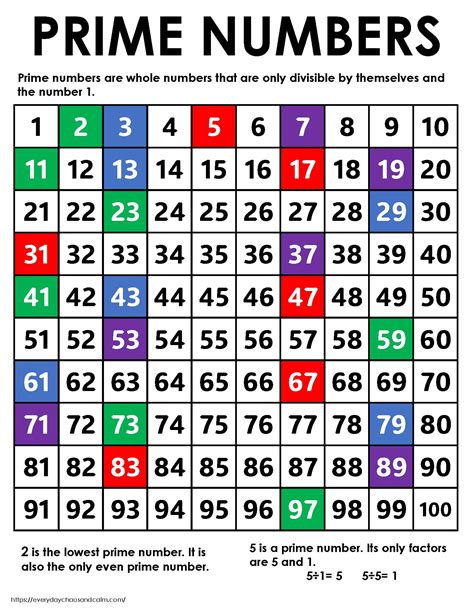
Prime numbers are the building blocks of all other numbers, as every positive integer can be expressed as a product of prime numbers in a unique way, known as the prime factorization. For example, the number 6 can be expressed as 2 * 3, where both 2 and 3 are prime numbers.
Checking if 29 is Prime
To check if 29 is a prime number, we need to see if it has any divisors other than 1 and 29. The number 29 is not divisible by 2, 3, 4, 5, and so on, up to its square root. The square root of 29 is approximately 5.385, so we only need to check divisibility up to 5, as any factor larger than the square root would have a corresponding factor smaller than the square root.
| Possible Divisors | Divisibility |
|---|---|
| 2 | Not divisible |
| 3 | Not divisible |
| 4 | Not divisible |
| 5 | Not divisible |
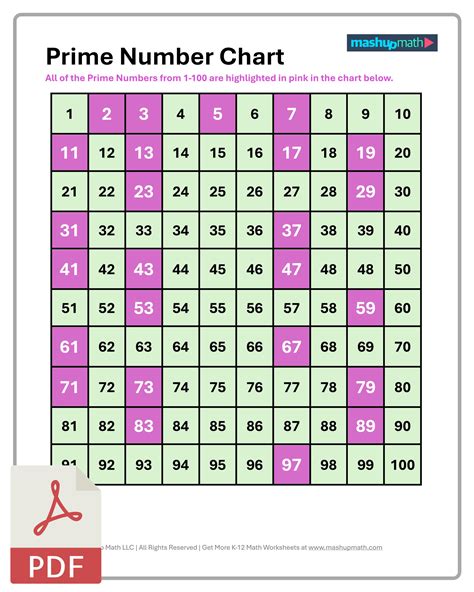
The process of checking for divisibility can be tedious for larger numbers, but for smaller numbers like 29, it's straightforward. The absence of divisors other than 1 and the number itself confirms that 29 is indeed a prime number.
Key Points
- Prime numbers are integers greater than 1 with only two distinct positive divisors: 1 and themselves.
- The number 29 has no divisors other than 1 and 29.
- Checking divisibility up to the square root of a number is sufficient to determine if it's prime.
- 29 meets the criteria for being a prime number based on its lack of divisors.
- Prime numbers play a crucial role in number theory and are fundamental to many mathematical concepts.
Importance of Prime Numbers
Prime numbers have significant importance in mathematics and computer science, particularly in cryptography. Many encryption algorithms, such as RSA, rely on the properties of prime numbers to ensure secure data transmission. Understanding prime numbers and their distribution is also crucial for advancing number theory and solving problems in other areas of mathematics.
Practical Applications
Beyond their theoretical significance, prime numbers have practical applications in coding theory, random number generation, and even in the design of computer networks. The study of prime numbers continues to be an active area of research, with new discoveries and methods for finding large prime numbers being developed regularly.
In conclusion, 29 is indeed a prime number, as it satisfies the definition of having no positive divisors other than 1 and itself. The understanding and identification of prime numbers are essential for various mathematical and computational applications, making them a fascinating and important area of study.
What is the definition of a prime number?
+A prime number is a positive integer greater than 1 that has no positive integer divisors other than 1 and itself.
Why are prime numbers important?
+Prime numbers are important because they are the building blocks of all other numbers and have significant applications in cryptography, coding theory, and other areas of mathematics and computer science.
How do you check if a number is prime?
+To check if a number is prime, you need to verify that it has no divisors other than 1 and itself. For larger numbers, this involves checking divisibility up to the square root of the number.