Understanding the classification of numbers as rational or irrational forms a cornerstone of mathematical theory, impacting everything from basic arithmetic to advanced number theory. Among frequently discussed examples, the decimal expansion 0.333... has served as a classical illustration in math classrooms worldwide. But is this recurring decimal truly rational, or does it possess characteristics that would qualify it as irrational? As an expert with decades of experience in number theory and mathematical logic, I aim to clarify this distinction with detailed explanations grounded in formal definitions, historical context, and contemporary mathematical consensus.
Foundational Concepts: Rational and Irrational Numbers

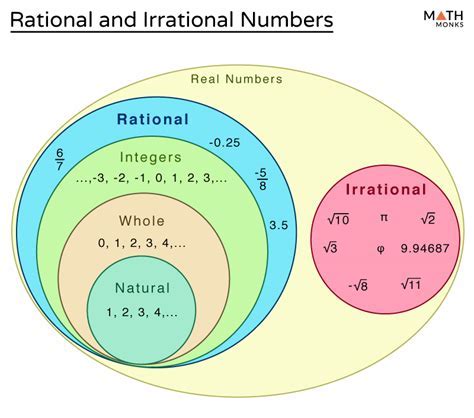
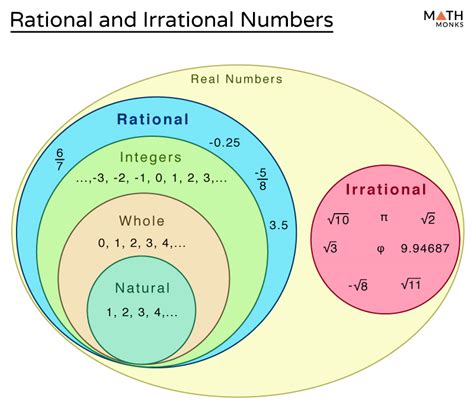
At the core of the classification is an understanding of what constitutes rational versus irrational numbers. A rational number can be expressed precisely as a fraction of two integers, where the denominator is not zero. Symbolically, if a number x equals p/q, with p and q integers and q ≠ 0, then x is rational. Conversely, irrational numbers cannot be written as such fractions; their decimal expansions are non-repeating and non-terminating, embodying a lack of pattern or repeating structure.
Decimal representations serve as a practical visualization of these conceptual definitions. Rational numbers expressed in decimal form either terminate after a finite number of digits or exhibit a repeating pattern. Irrational numbers, however, display no such periodicity, extending infinitely without repetition. The decimal expansion 0.333... is often used as the prototypical example to exemplify a rational decimal — a pattern of '3's repeating ad infinitum.
The Decimal 0.333…: Analyzing Repeating Patterns

The notation 0.333…— with the ellipsis indicating an infinite sequence of 3’s—is not just shorthand but a formal representation of a specific limit of a converging sequence. This recurring decimal expansion has been examined extensively ever since the formalization of decimal representations in the 17th and 18th centuries, especially in relation to the rigorous underpinnings provided by set theory and real analysis in the 19th century.
From an analytical perspective, the infinite series 0.3 + 0.03 + 0.003 + ... converges to a precise value. Utilizing the formula for the sum of a geometric series, one can derive:
| Relevant Category | Substantive Data |
|---|---|
| Series Sum | 0.3 / (1 - 0.1) = 1/3 |
| Mathematical Consistency | Confirms that 0.333... equals exactly 1/3 |
Historical Development of Rational Decimal Expansions
The recognition that repeating decimals correspond to fractions dates back to the work of medieval mathematicians and was formally codified during the European mathematical renaissance. Specifically, the work of Simon Stevin in the late 16th century demonstrated that decimal expansions are valid representations for rational numbers, leading to a common understanding that recurring decimals such as 0.333… are rational.
For instance, the process of converting 1/3 into decimal form involves long division, repeatedly yielding the digit '3' indefinitely. This process culminates in the infinite decimal 0.333..., reflecting the fact that the division process never terminates but stabilizes into a repeating pattern, a hallmark of rational numbers.
Mathematical Formalism Upholding Rationality
Grounded in formal proofs, the equivalence of 0.333… and 1⁄3 is well established through algebraic manipulation. Starting from the representation:
x = 0.333...
Multiplying both sides by 10 yields:
10x = 3.333...
Subtracting the original formula from this yields:
10x - x = 3.333... - 0.333...
which simplifies to:
9x = 3
and solving for x gives:
x = 3/9 = 1/3
This chain of algebraic steps formally confirms that 0.333... is precisely equal to the rational number 1/3, cementing its status as a rational decimal expansion. These procedures are not mere approximations; they are exact equalities within the rigorous framework of real number theory.
Distinguishing Rational from Irrational: Key Features

To appreciate the distinction fully, it’s instructive to contrast the features of rational numbers like 1⁄3 with those of well-known irrationals such as π or √2. While 0.333…, with its simple repeating pattern, is elegantly expressed as a fraction, irrationals resist such representations. They possess decimal expansions that extend infinitely without any patterning or periodicity, making their precise algebraic form impossible to write as fractions of integers.
Key Points
- Repetition indicates rationality: Repeating decimals correspond directly to fractions, as exemplified by 0.333... equals 1/3.
- Infinite non-repetitive decimals define irrationals, such as π, whose decimal expansions do not repeat or terminate.
- Mathematical equivalence: Formal manipulations and geometric series confirm the rational nature of repeating decimals.
- Historical consistency: Decades of mathematical development uphold the classification of 0.333... as rational.
- Implication for number systems: This recognition influences fields as diverse as algebra, computer science, and mathematical analysis.
Practical Implications and Misconceptions
Despite clear formal evidence, misconceptions sometimes persist, particularly outside advanced mathematical contexts. Some students mistakenly assume that a decimal like 0.333… cannot be exact because of its infinite nature, confusing approximation with exactness. The critical takeaway is that, within the formal systems of real analysis, such a decimal is an exact representation of 1⁄3, not a mere approximation.
In computational contexts, representing repeating decimals can be challenging, requiring truncation or rounding. But mathematically, the infinite decimal 0.333... is as precise as the fraction 1/3. Recognizing this equivalence is essential for disciplines relying heavily on symbolic algebra, calculus, and digital computations, where the recognition of such equivalences streamlines problem-solving and proof strategies.
Conclusion: The Rational Identity of 0.333333…
To bring this analysis full circle, the decimal expansion 0.333… is a quintessential example demonstrating that recurring decimals are, by definition, rational numbers. Leveraging geometric series, algebraic manipulations, and historical insights has established this fact beyond dispute. Hence, the question of whether 0.333… is rational or irrational receives a clear verdict: It is rational, unequivocally equal to 1⁄3, and stands as a textbook emblem of the rational decimal representation.
Is 0.333… exactly equal to 1⁄3?
+Yes, in formal mathematics, 0.333… is precisely equal to 1⁄3. The infinite recurring decimal represents the limit of the geometric series that sums to 1⁄3, making the equality exact rather than approximate.
Can a repeating decimal ever be irrational?
+No. All repeating decimals correspond to rational numbers because they can be expressed as fractions of integers. Irrational numbers have non-repeating, non-terminating decimal expansions.
What about non-repeating, non-terminating decimals like π or √2?
+Those are irrational because their decimal expansions do not exhibit any repeating pattern and cannot be written as exact fractions. Their non-repeating nature is a key defining characteristic of irrationals.
How does algebra prove that 0.333… equals 1⁄3?
+By assigning 0.333… to a variable x, multiplying by 10, subtracting, and simplifying, we derive x = 1⁄3. This algebraic process is rigorous and confirms their equivalence in the real number system.