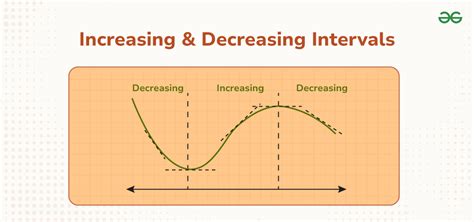
Understanding increasing and decreasing intervals is a fundamental concept in mathematics, particularly in calculus and analysis. It helps in identifying the behavior of functions, which is crucial in various applications, including physics, engineering, and economics. The concept revolves around determining the intervals where a function is either increasing or decreasing. In this article, we will delve into the world of increasing and decreasing intervals, exploring what they are, how to identify them, and their significance in mathematical analysis.
Key Points
- Definition and understanding of increasing and decreasing intervals
- Methods for identifying increasing and decreasing intervals of a function
- Importance of these intervals in calculus and real-world applications
- Practical examples illustrating the concept
- Techniques for analyzing functions to determine these intervals
Understanding Increasing and Decreasing Intervals
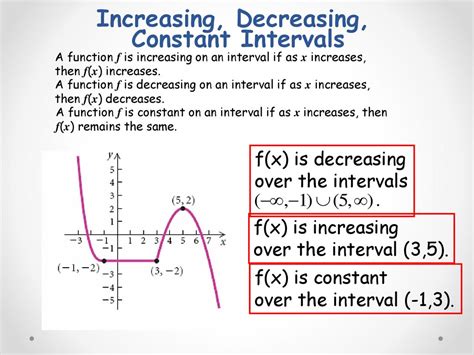
A function f(x) is said to be increasing on an interval if for any two points x1 and x2 in the interval, f(x1) ≤ f(x2) whenever x1 ≤ x2. Conversely, f(x) is decreasing on an interval if f(x1) ≥ f(x2) whenever x1 ≤ x2. These definitions form the basis of identifying the behavior of functions over different intervals.
Identifying Increasing and Decreasing Intervals
To identify whether a function is increasing or decreasing over an interval, one can use the first derivative of the function. If the derivative, f’(x), is positive over an interval, then the function is increasing in that interval. If f’(x) is negative, the function is decreasing. This method provides a systematic approach to analyzing the behavior of functions.
| Function Behavior | Derivative Sign |
|---|---|
| Increasing | Positive |
| Decreasing | Negative |
| Constant | Zero |
For example, consider the function f(x) = x^2. To find where this function is increasing or decreasing, we first find its derivative, f'(x) = 2x. f'(x) > 0 when x > 0, indicating that f(x) is increasing for x > 0. Similarly, f'(x) < 0 when x < 0, meaning f(x) is decreasing for x < 0.
Significance in Calculus and Applications

The concept of increasing and decreasing intervals is vital in calculus, as it helps in understanding the behavior of functions, which is critical in optimization problems, graphing functions, and understanding the physical world. In physics, for instance, the velocity of an object can be understood by analyzing the increasing and decreasing intervals of its position function over time.
Practical Applications
Beyond calculus, the concept has practical implications in economics, where understanding the behavior of supply and demand curves is essential for market analysis. In engineering, the stability of systems can be analyzed by examining the increasing and decreasing intervals of relevant functions, ensuring that systems operate within safe and efficient parameters.
The application of increasing and decreasing intervals extends to data analysis, where trends in data can be understood by identifying intervals where data is increasing or decreasing. This helps in forecasting future trends and making informed decisions based on historical data.
How do I determine if a function is increasing or decreasing at a point?
+To determine if a function is increasing or decreasing at a point, examine the sign of the derivative at that point. A positive derivative indicates the function is increasing, while a negative derivative indicates it is decreasing.
What is the significance of increasing and decreasing intervals in real-world applications?
+Understanding increasing and decreasing intervals is crucial in various real-world applications, including physics, engineering, and economics. It helps in analyzing trends, optimizing systems, and making informed decisions based on the behavior of functions over different intervals.
In conclusion, increasing and decreasing intervals are fundamental concepts in mathematics that provide valuable insights into the behavior of functions. By understanding and applying these concepts, individuals can better analyze and interpret data, optimize systems, and make informed decisions in a wide range of fields. Whether in calculus, physics, engineering, or economics, the ability to identify and apply the principles of increasing and decreasing intervals is a powerful tool for problem-solving and critical thinking.