Solving absolute value equations is a fundamental concept in algebra, and it can be straightforward once you understand the basic principles. Absolute value equations involve the absolute value of a variable or an expression, which can make them slightly more complex than linear equations. In this article, we will delve into the world of absolute value equations, exploring how to solve them with ease, and examining the underlying concepts that make them work.
Understanding Absolute Value
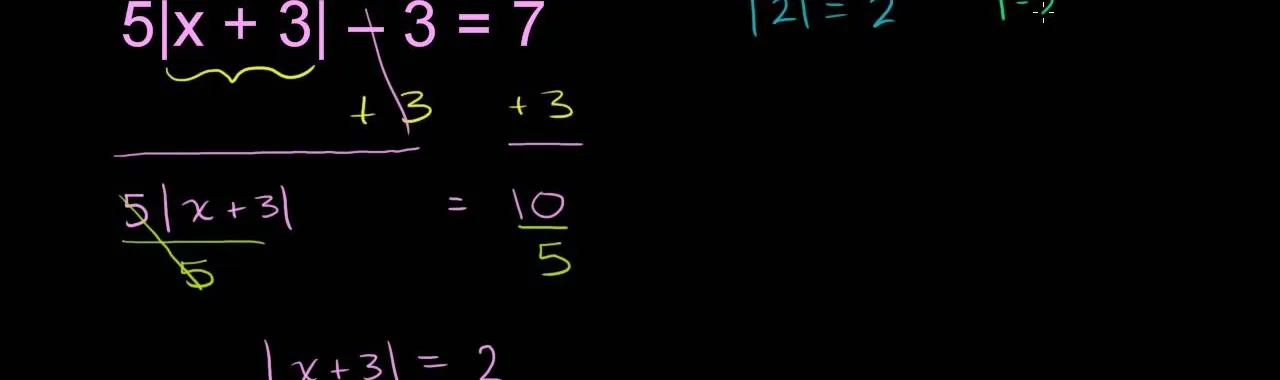
Absolute value is a mathematical concept that refers to the distance of a number from zero on the number line. It is denoted by two vertical lines, | |, and it is always non-negative. For example, the absolute value of 5 is |5| = 5, and the absolute value of -5 is |-5| = 5. This concept is crucial in solving absolute value equations, as it allows us to consider both positive and negative solutions.
Key Points
- Absolute value equations involve the absolute value of a variable or expression.
- The absolute value of a number is its distance from zero on the number line.
- Absolute value equations can have one or two solutions, depending on the equation.
- To solve absolute value equations, we need to consider both positive and negative cases.
- Graphical methods can also be used to solve absolute value equations.
Solving Simple Absolute Value Equations
Solving simple absolute value equations involves isolating the absolute value expression and then considering both positive and negative cases. For example, let’s solve the equation |x| = 4. To solve this equation, we need to consider two cases: x = 4 and x = -4. Both cases satisfy the equation, so the solutions are x = 4 and x = -4.
| Equation | Solutions |
|---|---|
| |x| = 4 | x = 4, x = -4 |
| |x - 2| = 3 | x = 5, x = -1 |
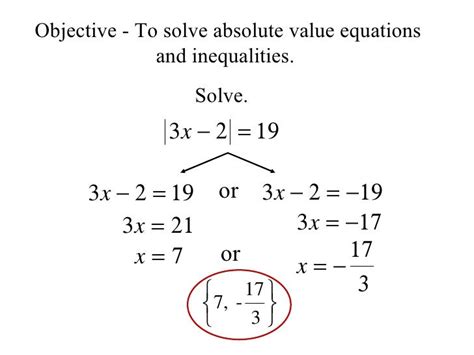
Solving More Complex Absolute Value Equations

More complex absolute value equations can be solved using the same principles as simple absolute value equations. However, we may need to use algebraic manipulations to isolate the absolute value expression. For example, let’s solve the equation |2x - 3| = 5. To solve this equation, we need to isolate the absolute value expression and then consider both positive and negative cases.
First, we can rewrite the equation as 2x - 3 = ±5. Then, we can add 3 to both sides to get 2x = 3 ± 5. Finally, we can divide both sides by 2 to get x = (3 ± 5)/2. This gives us two possible solutions: x = (3 + 5)/2 = 4 and x = (3 - 5)/2 = -1.
Graphical Methods for Solving Absolute Value Equations
Graphical methods can also be used to solve absolute value equations. By plotting the graph of the absolute value function, we can visually identify the solutions to the equation. For example, let’s solve the equation |x| = 4 using graphical methods. We can plot the graph of the absolute value function and then find the points where the graph intersects the line y = 4. These points correspond to the solutions x = 4 and x = -4.
Common Challenges and Mistakes
When solving absolute value equations, there are several common challenges and mistakes to watch out for. One common mistake is forgetting to consider both positive and negative cases. This can lead to missing potential solutions and incorrect answers. Another challenge is dealing with complex absolute value equations that involve algebraic manipulations. In these cases, it’s essential to carefully isolate the absolute value expression and consider both positive and negative cases.
What is the main concept behind absolute value equations?
+The main concept behind absolute value equations is the absolute value of a variable or expression, which can be positive or negative.
How do I solve simple absolute value equations?
+To solve simple absolute value equations, isolate the absolute value expression and consider both positive and negative cases.
What are some common challenges and mistakes when solving absolute value equations?
+Common challenges and mistakes include forgetting to consider both positive and negative cases, and dealing with complex absolute value equations that involve algebraic manipulations.
In conclusion, solving absolute value equations can be straightforward once you understand the basic principles. By considering both positive and negative cases, using algebraic manipulations, and graphical methods, you can easily solve absolute value equations and unlock the secrets of algebra. Remember to watch out for common challenges and mistakes, and always double-check your solutions to ensure accuracy.



