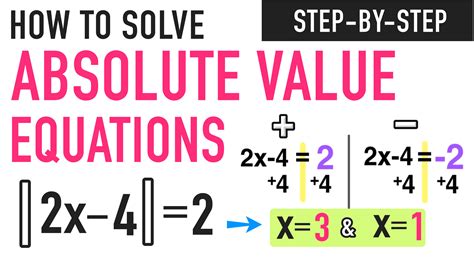Absolute value is a fundamental concept in mathematics that represents the distance of a number from zero on the number line, regardless of direction. It is denoted by two vertical lines, | |, and is defined as the non-negative value of a number. For instance, the absolute value of 5 is |5| = 5, and the absolute value of -5 is |-5| = 5. In this article, we will delve into the world of absolute value, exploring its definition, properties, and applications, as well as providing step-by-step guides on how to solve absolute value equations and inequalities.
Key Points
- Absolute value represents the distance of a number from zero on the number line.
- The absolute value of a number is always non-negative.
- Absolute value equations have two solutions, one positive and one negative.
- Absolute value inequalities can be solved using the properties of absolute value.
- Absolute value has numerous applications in physics, engineering, and computer science.
Definition and Properties of Absolute Value
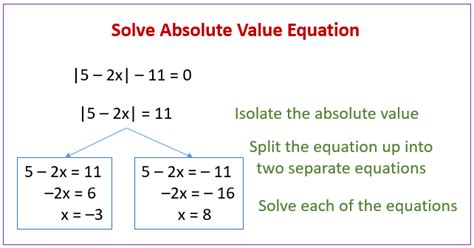
The absolute value of a real number x, denoted by |x|, is defined as the non-negative value of x, without regard to its sign. It can be expressed as |x| = x if x ≥ 0, and |x| = -x if x < 0. The absolute value has several important properties, including the fact that it is always non-negative, and that the absolute value of a product is the product of the absolute values.
Absolute Value Equations
An absolute value equation is an equation that contains an absolute value expression. To solve an absolute value equation, we need to consider two cases: one where the expression inside the absolute value is positive, and one where it is negative. For example, to solve the equation |x| = 5, we would consider the cases x = 5 and x = -5. This is because the absolute value of x is 5 in both cases.
| Type of Equation | Example | Solution |
|---|---|---|
| Simple Absolute Value Equation | |x| = 5 | x = 5 or x = -5 |
| Absolute Value Equation with Variable Expression | |2x - 3| = 7 | 2x - 3 = 7 or 2x - 3 = -7 |

Absolute Value Inequalities
Absolute value inequalities are inequalities that contain an absolute value expression. To solve an absolute value inequality, we need to consider two cases: one where the expression inside the absolute value is positive, and one where it is negative. For example, to solve the inequality |x| < 5, we would consider the cases -5 < x < 5. This is because the absolute value of x is less than 5 in this range.
Applications of Absolute Value

Absolute value has numerous applications in various fields, including physics, engineering, and computer science. In physics, absolute value is used to represent the magnitude of physical quantities such as velocity, acceleration, and force. In engineering, absolute value is used to design and optimize systems, such as electronic circuits and mechanical systems. In computer science, absolute value is used in algorithms and data structures, such as sorting and searching algorithms.
Real-World Examples
Absolute value is used in many real-world applications, such as calculating distances, velocities, and accelerations. For example, the distance between two cities can be represented as the absolute value of the difference between their coordinates. The velocity of an object can be represented as the absolute value of its rate of change of position. The acceleration of an object can be represented as the absolute value of its rate of change of velocity.
What is the definition of absolute value?
+Absolute value is a measure of the distance of a number from zero on the number line, regardless of direction.
How do I solve an absolute value equation?
+To solve an absolute value equation, consider two cases: one where the expression inside the absolute value is positive, and one where it is negative.
What are some real-world applications of absolute value?
+Absolute value has numerous applications in physics, engineering, and computer science, including calculating distances, velocities, and accelerations.
In conclusion, absolute value is a fundamental concept in mathematics that has numerous applications in various fields. By understanding the definition, properties, and applications of absolute value, you can solve absolute value equations and inequalities with ease, and apply this knowledge to real-world problems. Whether you’re a student, teacher, or professional, mastering absolute value is essential for success in mathematics and related fields.