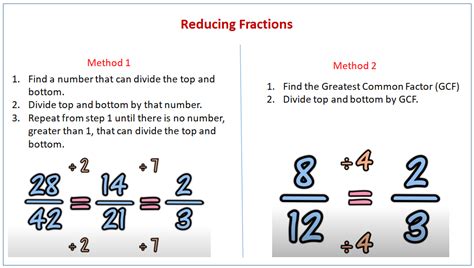
Reducing fractions is a fundamental concept in mathematics that involves simplifying a fraction to its lowest terms. This process is essential for making calculations easier and more efficient. In this article, we will explore five ways to reduce fractions, providing a comprehensive understanding of the methods and their applications.
Key Points
- Understanding the concept of greatest common divisor (GCD) for reducing fractions
- Applying the prime factorization method for fraction reduction
- Using the division method for simplifying fractions
- Employing the cancellation method for reducing fractions
- Utilizing online tools and calculators for efficient fraction reduction
Understanding the Concept of Greatest Common Divisor (GCD)

The greatest common divisor (GCD) is the largest number that divides both the numerator and the denominator of a fraction without leaving a remainder. To reduce a fraction, we need to find the GCD of the numerator and the denominator and divide both numbers by the GCD. For example, to reduce the fraction 12⁄18, we find the GCD of 12 and 18, which is 6. Then, we divide both 12 and 18 by 6 to get the reduced fraction 2⁄3.
Applying the Prime Factorization Method
The prime factorization method involves breaking down the numerator and the denominator into their prime factors and then canceling out common factors. For instance, to reduce the fraction 24⁄36, we break down 24 into 2^3 * 3 and 36 into 2^2 * 3^2. We can then cancel out the common factors, which are 2^2 and 3, to get the reduced fraction 2⁄3.
| Method | Description |
|---|---|
| GCD Method | Find the GCD of the numerator and the denominator and divide both numbers by the GCD |
| Prime Factorization Method | Break down the numerator and the denominator into their prime factors and cancel out common factors |
| Division Method | Divide the numerator by the denominator and simplify the resulting fraction |
| Cancellation Method | Cancel out common factors between the numerator and the denominator |
| Online Tools and Calculators | Use online tools and calculators to efficiently reduce fractions |
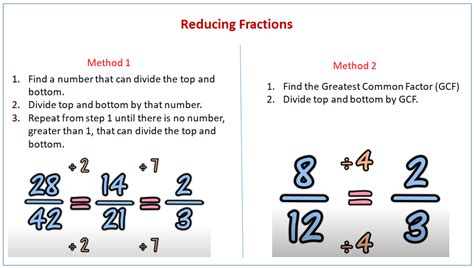
Using the Division Method

The division method involves dividing the numerator by the denominator and simplifying the resulting fraction. For example, to reduce the fraction 20⁄25, we can divide 20 by 25 to get 0.8. We can then simplify 0.8 to get the reduced fraction 4⁄5.
Employing the Cancellation Method
The cancellation method involves canceling out common factors between the numerator and the denominator. For instance, to reduce the fraction 15⁄20, we can cancel out the common factor 5 to get the reduced fraction 3⁄4.
Utilizing Online Tools and Calculators
With the advancement of technology, there are now various online tools and calculators available that can efficiently reduce fractions. These tools can save time and effort, especially when dealing with complex fractions. However, it is essential to understand the underlying methods and concepts to ensure accuracy and reliability.
What is the importance of reducing fractions?
+Reducing fractions is essential for making calculations easier and more efficient. It helps to avoid errors and ensures that the resulting fraction is in its simplest form.
How can I reduce a fraction using the GCD method?
+To reduce a fraction using the GCD method, find the GCD of the numerator and the denominator and divide both numbers by the GCD. For example, to reduce the fraction 12/18, find the GCD of 12 and 18, which is 6. Then, divide both 12 and 18 by 6 to get the reduced fraction 2/3.
Can I use online tools and calculators to reduce fractions?
+Yes, there are various online tools and calculators available that can efficiently reduce fractions. These tools can save time and effort, especially when dealing with complex fractions. However, it is essential to understand the underlying methods and concepts to ensure accuracy and reliability.
In conclusion, reducing fractions is a crucial concept in mathematics that involves simplifying a fraction to its lowest terms. By understanding the different methods, such as the GCD method, prime factorization method, division method, cancellation method, and utilizing online tools and calculators, individuals can efficiently reduce fractions and make calculations easier and more efficient.