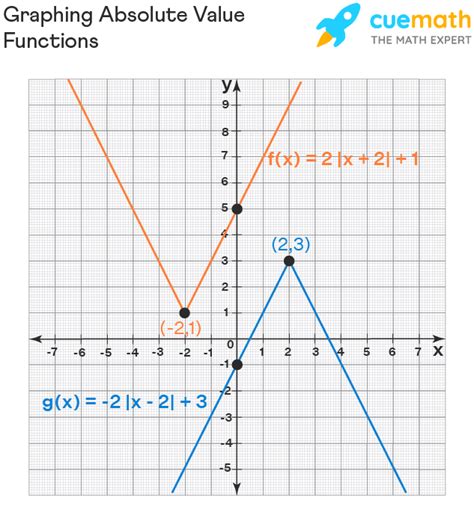
The concept of absolute value is a fundamental aspect of mathematics, particularly in graphing and analyzing functions. When dealing with graphing absolute value, it's essential to understand how the absolute value function affects the graph of an equation. In this article, we will explore five ways to graph absolute value functions, providing a comprehensive understanding of the subject matter.
Introduction to Absolute Value Functions
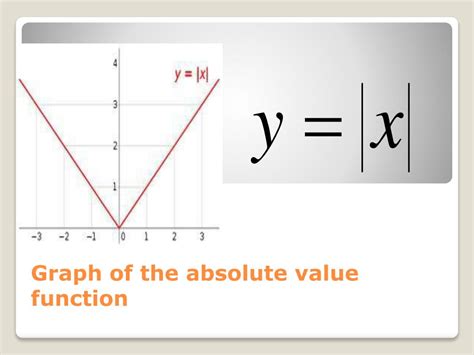
Absolute value functions are defined as f(x) = |x|, where the output is always non-negative. When graphing absolute value functions, it’s crucial to consider the definition of absolute value and how it impacts the graph. The absolute value function can be broken down into two cases: x ≥ 0 and x < 0. For x ≥ 0, the function is equivalent to f(x) = x, while for x < 0, the function becomes f(x) = -x.
Key Points
- The absolute value function is defined as f(x) = |x|.
- The function can be broken down into two cases: x ≥ 0 and x < 0.
- For x ≥ 0, the function is equivalent to f(x) = x.
- For x < 0, the function becomes f(x) = -x.
- Understanding the definition of absolute value is crucial for graphing absolute value functions.
Method 1: Graphing Absolute Value Functions Using the Definition

One way to graph absolute value functions is by using the definition of absolute value. This method involves breaking down the function into two cases: x ≥ 0 and x < 0. For x ≥ 0, the function is graphed as f(x) = x, while for x < 0, the function is graphed as f(x) = -x. By combining these two graphs, we can obtain the graph of the absolute value function.
For example, consider the function f(x) = |x|. Using the definition of absolute value, we can break down the function into two cases:
Case 1: x ≥ 0
f(x) = x
Case 2: x < 0
f(x) = -x
By graphing these two cases, we can obtain the graph of the absolute value function.
Example: Graphing f(x) = |x|
To graph the function f(x) = |x|, we can use the definition of absolute value. For x ≥ 0, the function is graphed as f(x) = x, while for x < 0, the function is graphed as f(x) = -x. The resulting graph is a V-shaped graph with its vertex at the origin (0, 0).
| x | f(x) = |x| |
|---|---|
| -3 | 3 |
| -2 | 2 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |

Method 2: Graphing Absolute Value Functions Using Transformations
Another way to graph absolute value functions is by using transformations. This method involves graphing the function f(x) = x and then reflecting the graph about the x-axis for x < 0. By applying this transformation, we can obtain the graph of the absolute value function.
For example, consider the function f(x) = |x|. To graph this function using transformations, we can start by graphing the function f(x) = x. Then, we can reflect the graph about the x-axis for x < 0. The resulting graph is a V-shaped graph with its vertex at the origin (0, 0).
Example: Graphing f(x) = |x| Using Transformations
To graph the function f(x) = |x| using transformations, we can start by graphing the function f(x) = x. Then, we can reflect the graph about the x-axis for x < 0. The resulting graph is a V-shaped graph with its vertex at the origin (0, 0).
Method 3: Graphing Absolute Value Functions Using the Parent Function
A third way to graph absolute value functions is by using the parent function. The parent function of an absolute value function is f(x) = x. By using the parent function, we can obtain the graph of the absolute value function by reflecting the graph about the x-axis for x < 0.
For example, consider the function f(x) = |x|. The parent function of this function is f(x) = x. By reflecting the graph of the parent function about the x-axis for x < 0, we can obtain the graph of the absolute value function.
Example: Graphing f(x) = |x| Using the Parent Function
To graph the function f(x) = |x| using the parent function, we can start by graphing the function f(x) = x. Then, we can reflect the graph about the x-axis for x < 0. The resulting graph is a V-shaped graph with its vertex at the origin (0, 0).
Method 4: Graphing Absolute Value Functions Using a Table of Values
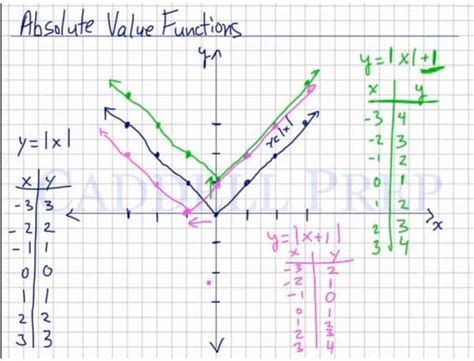
A fourth way to graph absolute value functions is by using a table of values. This method involves creating a table of x-values and corresponding y-values to graph the function. By using a table of values, we can obtain a clear understanding of the graph and its properties.
For example, consider the function f(x) = |x|. To graph this function using a table of values, we can create a table of x-values and corresponding y-values.
| x | f(x) = |x| |
|---|---|
| -3 | 3 |
| -2 | 2 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
Example: Graphing f(x) = |x| Using a Table of Values
To graph the function f(x) = |x| using a table of values, we can create a table of x-values and corresponding y-values. By plotting the points on the coordinate plane, we can obtain the graph of the absolute value function.
Method 5: Graphing Absolute Value Functions Using Technology
A fifth way to graph absolute value functions is by using technology, such as graphing calculators or computer software. This method involves entering the function into the technology and using it to graph the function. By using technology, we can obtain a clear understanding of the graph and its properties.
For example, consider the function f(x) = |x|. To graph this function using technology, we can enter the function into a graphing calculator or computer software. The resulting graph is a V-shaped graph with its vertex at the origin (0, 0).
Example: Graphing f(x) = |x| Using Technology
To graph the function f(x) = |x| using technology, we can enter the function into a graphing calculator or computer software. By using the technology to graph the function, we can obtain a clear understanding of the graph and its properties.
What is the definition of absolute value?
+The definition of absolute value is f(x) = |x|, where the output is always non-negative.
How do you graph absolute value functions?
+There are several ways to graph absolute value functions, including using the definition, transformations, the parent function, a table of values, and technology.
What is the parent function of an absolute value function?
+The parent function of an absolute value function is f(x) = x.
How do you use a table of values to graph an absolute value function?
+To use a table of values to graph an absolute value function, create a table of x-values and corresponding y-values, and then plot the points on the coordinate plane.
What is the benefit of using technology to graph absolute value functions?
+The benefit of using technology to graph absolute value functions is that it allows for quick and accurate graphing, and can help to identify key features of the graph.
Meta description: Learn how to graph absolute value functions using five different methods, including the definition, transformations, the parent function, a table of values, and technology.