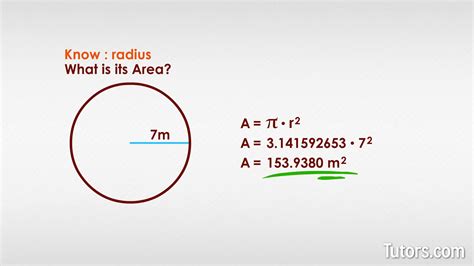
Calculating the area of a circle is a fundamental concept in geometry, and it's essential for various applications in mathematics, physics, engineering, and design. The formula to find the area of a circle is straightforward, but it's crucial to understand the underlying principles and the variables involved. In this article, we'll delve into the world of circles, explore the concept of area, and provide a step-by-step guide on how to calculate the area of a circle easily.
Key Points
- The formula to calculate the area of a circle is A = πr^2, where A is the area and r is the radius.
- The value of π (pi) is approximately 3.14159, but it's an irrational number, which means it cannot be expressed as a finite decimal or fraction.
- The radius of a circle is the distance from the center to the edge, and it's a critical variable in calculating the area.
- There are various methods to calculate the area of a circle, including using the diameter, circumference, or even the area of a sector.
- Understanding the concept of area and how to calculate it is essential for various applications, including design, engineering, and physics.
Understanding the Concept of Area
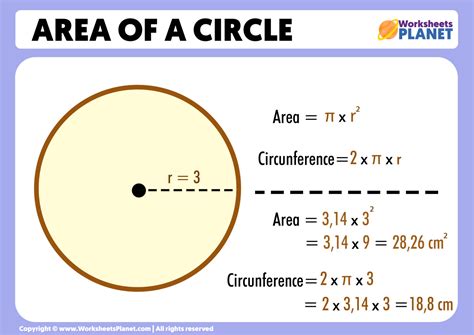
The area of a circle is the amount of space inside the circle, and it’s typically measured in square units, such as square meters or square inches. The concept of area is closely related to the concept of circumference, which is the distance around the circle. To calculate the area of a circle, you need to know the radius, which is the distance from the center to the edge.
What is Pi (π)?
Pi (π) is a mathematical constant that represents the ratio of a circle’s circumference to its diameter. It’s approximately equal to 3.14159, but it’s an irrational number, which means it cannot be expressed as a finite decimal or fraction. Pi is a fundamental constant in mathematics, and it’s essential for calculating the area and circumference of circles.
| Variable | Description | Value |
|---|---|---|
| π (pi) | Mathematical constant representing the ratio of a circle's circumference to its diameter | Approximately 3.14159 |
| r | Radius of the circle | Distance from the center to the edge |
| A | Area of the circle | A = πr^2 |

Calculating the Area of a Circle
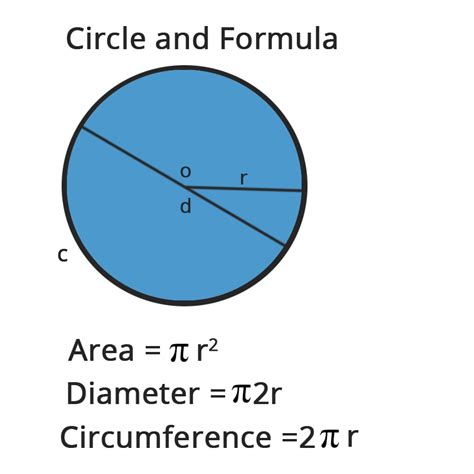
Now that we’ve covered the basics, let’s dive into the calculation. The formula to calculate the area of a circle is A = πr^2, where A is the area and r is the radius. Simply plug in the value of the radius, square it, and multiply it by pi (π). For example, if the radius is 4 inches, the area would be A = π(4)^2 = 3.14159 x 16 = 50.26548 square inches.
Using the Diameter to Calculate the Area
If you don’t know the radius, you can use the diameter to calculate the area. The diameter is twice the radius, so you can divide the diameter by 2 to get the radius. Then, use the formula A = πr^2 to calculate the area. For example, if the diameter is 8 inches, the radius would be 4 inches (8 / 2 = 4), and the area would be A = π(4)^2 = 50.26548 square inches.
Real-World Applications
Calculating the area of a circle has numerous real-world applications, including design, engineering, and physics. For example, architects use the area of a circle to design circular buildings, bridges, and tunnels. Engineers use the area to calculate the stress and strain on circular structures, such as pipes and cylinders. Physicists use the area to calculate the properties of circular objects, such as the area of a circle in a magnetic field.
What is the formula to calculate the area of a circle?
+The formula to calculate the area of a circle is A = πr^2, where A is the area and r is the radius.
What is the value of pi (π)?
+Pi (π) is approximately equal to 3.14159, but it's an irrational number, which means it cannot be expressed as a finite decimal or fraction.
How do I calculate the area of a circle using the diameter?
+To calculate the area of a circle using the diameter, divide the diameter by 2 to get the radius, and then use the formula A = πr^2.
In conclusion, calculating the area of a circle is a fundamental concept in geometry, and it’s essential for various applications in mathematics, physics, engineering, and design. By understanding the concept of area, the value of pi (π), and the formula A = πr^2, you can easily calculate the area of a circle. Remember to use the correct units, and don’t hesitate to reach out if you have any questions or need further clarification.