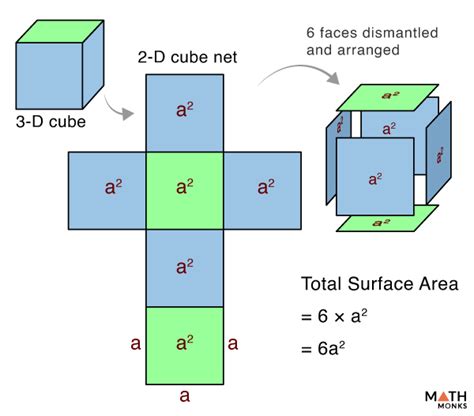
The cube surface area formula is a fundamental concept in geometry, used to calculate the total surface area of a cube. A cube is a three-dimensional solid object with six square faces of equal size, where each face is a square with equal length and width. The formula to calculate the surface area of a cube is straightforward and is based on the length of one side of the cube.
Understanding the Cube Surface Area Formula
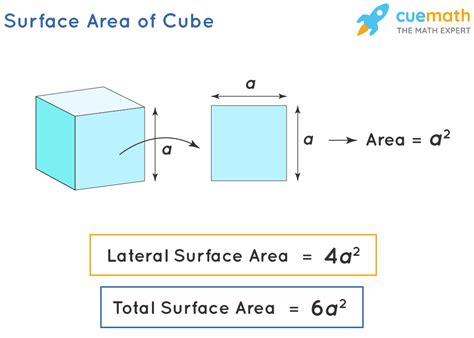
The formula for the surface area of a cube is given by 6s^2, where s is the length of one side of the cube. This formula is derived from the fact that a cube has six faces, and each face has an area of s^2. Since all faces are identical, the total surface area is calculated by multiplying the area of one face by the total number of faces, which is six.
Derivation of the Cube Surface Area Formula
To understand the derivation of the formula, consider a cube with each side having a length of ’s’. The area of one face of the cube is s * s, which equals s^2. Since the cube has six such faces, the total surface area is the sum of the areas of all six faces. Therefore, the total surface area = s^2 + s^2 + s^2 + s^2 + s^2 + s^2, which simplifies to 6s^2.
| Variable | Description |
|---|---|
| s | Length of one side of the cube |
| 6s^2 | Formula for the surface area of a cube |
Key Points
- The formula for the surface area of a cube is 6s^2, where s is the length of one side.
- A cube has six square faces, each with an area of s^2.
- The total surface area of a cube is the sum of the areas of all six faces.
- Ensuring all sides of the cube are equal in length is crucial for accurate surface area calculation.
- The cube surface area formula is used in various applications, including architecture, engineering, and design.
Applications of the Cube Surface Area Formula
The cube surface area formula has numerous practical applications. In architecture, it is used to calculate the surface area of cubic structures or components of buildings. In engineering, it is applied in the design of cubic containers, compartments, or machinery parts. Additionally, in packaging design, understanding the surface area of cubic boxes is essential for optimizing packaging materials and reducing waste.
Example Calculation
For example, if you have a cube with each side measuring 5 cm, the surface area would be calculated as 6 * (5 cm)^2 = 6 * 25 cm^2 = 150 cm^2. This means the total surface area of the cube is 150 square centimeters.
In conclusion, the cube surface area formula is a fundamental geometric concept with widespread applications. Its simplicity and utility make it an essential tool for professionals and students alike. By understanding and applying this formula, one can efficiently calculate the surface area of cubes, contributing to more accurate designs and calculations in various fields.
What is the formula for the surface area of a cube?
+The formula for the surface area of a cube is 6s^2, where s is the length of one side of the cube.
How do you derive the cube surface area formula?
+The formula is derived from the fact that a cube has six faces, each with an area of s^2. The total surface area is the sum of the areas of all six faces, which equals 6s^2.
What are some practical applications of the cube surface area formula?
+The cube surface area formula is used in architecture, engineering, design, and packaging to calculate the surface area of cubic structures or objects, aiding in material optimization and waste reduction.