Calculations are an essential part of various fields, including mathematics, physics, engineering, and finance. The ability to calculate accurately and efficiently is crucial for making informed decisions and solving complex problems. In this article, we will explore five ways to calculate, highlighting the importance of each method and providing examples of their applications.
Key Points
- Understanding the concept of arithmetic calculations and their applications
- Learning about geometric calculations and their role in problem-solving
- Exploring trigonometric calculations and their importance in physics and engineering
- Discovering the significance of statistical calculations in data analysis
- Mastering algebraic calculations and their applications in various fields
Arithmetic Calculations

Arithmetic calculations involve basic mathematical operations such as addition, subtraction, multiplication, and division. These operations are the foundation of mathematics and are used in various aspects of life, from simple calculations to complex problem-solving. Arithmetic calculations are essential in finance, where they are used to calculate interest rates, investments, and expenses.
For example, calculating the total cost of a product, including taxes and discounts, requires arithmetic operations. Accurate arithmetic calculations are crucial in ensuring that financial transactions are correct and efficient. Furthermore, arithmetic calculations are used in science and engineering to calculate quantities such as velocity, acceleration, and force.
Geometric Calculations
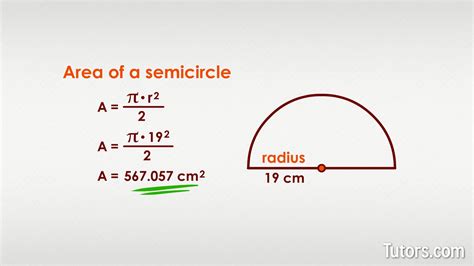
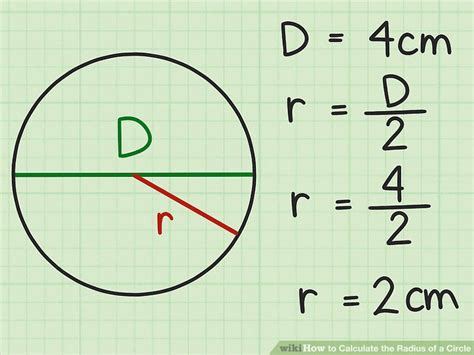
Geometric calculations involve the study of shapes and their properties. These calculations are used to determine the area, perimeter, and volume of various shapes, including triangles, circles, and rectangles. Geometric calculations are essential in architecture, engineering, and design, where they are used to create blueprints and models of buildings and structures.
For instance, calculating the area of a room or the volume of a container requires geometric calculations. Understanding geometric concepts such as points, lines, and angles is crucial in solving problems related to shape and space. Additionally, geometric calculations are used in computer graphics and game development to create 3D models and simulations.
| Type of Calculation | Example |
|---|---|
| Arithmetic | Calculating the total cost of a product |
| Geometric | Calculating the area of a room |
| Trigonometric | Calculating the height of a building |
| Statistical | Calculating the average score of a test |
| Algebraic | Calculating the value of x in an equation |
Trigonometric Calculations
Trigonometric calculations involve the study of triangles and their relationships. These calculations are used to determine the lengths of sides and the measures of angles in triangles. Trigonometric calculations are essential in physics and engineering, where they are used to calculate quantities such as force, velocity, and acceleration.
For example, calculating the height of a building or the distance of a ship from the shore requires trigonometric calculations. Understanding trigonometric concepts such as sine, cosine, and tangent is crucial in solving problems related to right triangles and circular motion. Additionally, trigonometric calculations are used in navigation and surveying to determine the position and distance of objects.
Statistical Calculations
Statistical calculations involve the analysis of data and the calculation of probabilities. These calculations are used to determine the average, median, and standard deviation of a dataset, as well as the probability of an event occurring. Statistical calculations are essential in data analysis and interpretation, where they are used to make informed decisions and predictions.
For instance, calculating the average score of a test or the probability of a customer purchasing a product requires statistical calculations. Understanding statistical concepts such as mean, median, and mode is crucial in solving problems related to data analysis and interpretation. Additionally, statistical calculations are used in finance and economics to calculate risks and predict market trends.
Algebraic Calculations
Algebraic calculations involve the study of variables and their relationships. These calculations are used to solve equations and inequalities, and to determine the value of unknown variables. Algebraic calculations are essential in various fields, including physics, engineering, and computer science, where they are used to model and analyze complex systems.
For example, calculating the value of x in an equation or the value of a function requires algebraic calculations. Understanding algebraic concepts such as variables, constants, and functions is crucial in solving problems related to equations and inequalities. Additionally, algebraic calculations are used in cryptography and coding theory to develop secure encryption algorithms and error-correcting codes.
What is the importance of arithmetic calculations in finance?
+Arithmetic calculations are essential in finance, as they are used to calculate interest rates, investments, and expenses. Accurate arithmetic calculations ensure that financial transactions are correct and efficient.
How are geometric calculations used in architecture and engineering?
+Geometric calculations are used in architecture and engineering to create blueprints and models of buildings and structures. These calculations determine the area, perimeter, and volume of various shapes, including triangles, circles, and rectangles.
What is the role of trigonometric calculations in physics and engineering?
+Trigonometric calculations are used in physics and engineering to calculate quantities such as force, velocity, and acceleration. These calculations determine the lengths of sides and the measures of angles in triangles, and are essential in solving problems related to right triangles and circular motion.
Meta description suggestion: “Discover the importance of arithmetic, geometric, trigonometric, statistical, and algebraic calculations in various fields, and learn how to apply these methods to solve complex problems.” (145 characters)